题目内容
如图，四边形ABCD是平行四边形，点E、F分别在BD上，且BE=DF．求证：AC、EF互相平分．
考点：平行四边形的判定与性质
专题：证明题
分析：接AE、CF．根据DF=EB且平行证明四边形AECF是平行四边形．再根据平行四边形的性质：对角线互相平分得到AC与EF互相平分．
解答：证明：连接AE、CF，
∵四边形 ABCD 是平行四边形，
∴AD=BC，AD∥BC，
∵BE=DF，
∴AD-DF=BC-BE，
∴AF=CE，
∵AF∥CE，
∴四边形AECF是平行四边形，
∴AC、EF互相平分．
∵四边形 ABCD 是平行四边形，
∴AD=BC，AD∥BC，
∵BE=DF，
∴AD-DF=BC-BE，
∴AF=CE，
∵AF∥CE，
∴四边形AECF是平行四边形，
∴AC、EF互相平分．
点评：本题考查了平行四边形的判定与性质，熟练掌握性质定理和判定定理是解题的关键．平行四边形的五种判定方法与平行四边形的性质相呼应，每种方法都对应着一种性质，在应用时应注意它们的区别与联系．
练习册系列答案
中考解读考点精练系列答案
相关题目
关于x的方程x2+2kx+k-1=0的根的情况描述正确的是（ ）
| A、k为任何实数，方程都有实根 |
| B、k为任何实数，方程都有两个不相等的实根 |
| C、k为任何实数，方程都有两个相等的实根 |
| D、以上说法都对 |
计算（2+1）（22+1）（24+1）（28+1）得（ ）
| A、28-1 |
| B、210-1 |
| C、216-1 |
| D、232-1 |
2.796精确到百分位的结果是（ ）
| A、2.79 | B、2.81 |
| C、2.7 | D、2.80 |
下列说法正确的是（ ）
| A、3是-9的算术平方根 |
| B、-3是（-3）2的算术平方根 |
| C、8的立方根是±2 |
| D、16的平方根是±4 |
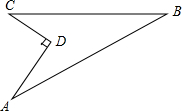如图，某住宅小区在施工过程中留下了一块空地，已知AD=4米，CD=3米，∠ADC=90°，AB=13米，BC=12米，小区为美化环境，欲在空地上铺草坪，已知草坪每平方米100元，试问用该草坪铺满这块空地共需花费多少元？
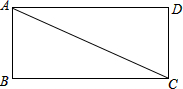如图，有一个长方形花园，对角线AC是一条小路，现要在AD边上找一个位置建报亭，使报亭到小路两端点A、C的距离相等．