题目内容
3.解不等式组$\left\{\begin{array}{l}{3x+2>5x-4①}\\{\frac{2x+3}{3}≥\frac{1}{2}x+1②}\end{array}\right.$,并判断2$\sqrt{3}$是否为此不等组的解.分析 分别求出每一个不等式的解集,根据口诀:大小小大中间找,确定不等式组的解集,再判断2$\sqrt{3}$是否在此范围内即可.
解答 解:解不等式①得,x<3;
解不等式②得,x≥0.
∴不等式组的解集为:0≤x<3.
∵2$\sqrt{3}$≈2×1.732=3.464>3,
∴2$\sqrt{3}$不是此不等组的解.
点评 本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
14.下列图形不一定是轴对称图形的是( )
| A. | 直角三角形 | B. | 钝角 | C. | 线段 | D. | 圆 |
11. 如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )
如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )
 如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )
如图,点O是平行四边形ABCD的对角线的交点,则图中全等三角形共有( )| A. | 4对 | B. | 3对 | C. | 2对 | D. | 1对 |
18.下列调查中,适合采用抽样调查的是( )
| A. | 对乘坐某班次飞机的乘客进行安检 | |
| B. | 了解一批节能灯管的使用寿命 | |
| C. | 选出某班学生中跑的最快的学生参加全县比赛 | |
| D. | 了解一班同学的视力情况 |
8. 如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
 如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )
如图,?ABCD中,AB=4,BC=3,∠DCB=30°,动点E从B点出发,沿B-C-D-A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数图象用图象表示正确的是( )| A. | 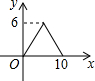 | B. |  | C. | 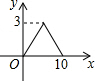 | D. | 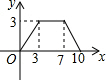 |
12. 如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
 如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )| A. | SAS | B. | ASA | C. | AAS | D. | SSS |
13. 为提高课堂效率,引导学生积极参与课堂教学,鼓励学生大胆发言,勇于发表自己的观点促进自主前提下的小组合作学习,张老师调查统计了一节课学生回答问题的次数(如图所示)这次调查统计的数据的众数和中位数分别是( )
为提高课堂效率,引导学生积极参与课堂教学,鼓励学生大胆发言,勇于发表自己的观点促进自主前提下的小组合作学习,张老师调查统计了一节课学生回答问题的次数(如图所示)这次调查统计的数据的众数和中位数分别是( )
 为提高课堂效率,引导学生积极参与课堂教学,鼓励学生大胆发言,勇于发表自己的观点促进自主前提下的小组合作学习,张老师调查统计了一节课学生回答问题的次数(如图所示)这次调查统计的数据的众数和中位数分别是( )
为提高课堂效率,引导学生积极参与课堂教学,鼓励学生大胆发言,勇于发表自己的观点促进自主前提下的小组合作学习,张老师调查统计了一节课学生回答问题的次数(如图所示)这次调查统计的数据的众数和中位数分别是( )| A. | 众数2,中位数3 | B. | 众数2,中位数2.5 | C. | 众数3,中位数2 | D. | 众数4,中位数3 |
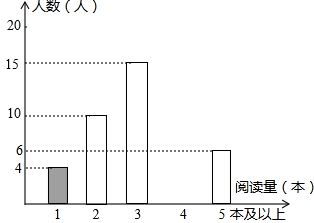 某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题:
某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题: 如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△AEC=S△ABC,其中正确结论有( )个.
如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF;②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△AEC=S△ABC,其中正确结论有( )个.