题目内容
19．已知4n-m=4，则（m-4n）2-3（m-4n）-10的值是（ ）| A． | -6 | B． | 6 | C． | 18 | D． | -38 |
分析 首先把：（m-4n）2-3（m-4n）-10变形为（4n-m）2+3（4n-m）-10，然后再代入4n-m=4即可．
解答 解：（m-4n）2-3（m-4n）-10，
=（4n-m）2+3（4n-m）-10，
=42+3×4-10，
=16+12-10，
=18，
故选：C．
点评 此题主要考查了代数式求值，关键是正确找出代数式和所给条件的关系．
练习册系列答案
相关题目
20．
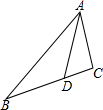如图，在△ABC中，点D在边BC上，若∠BAD=∠CAD，AB=6，AC=3，S△ABD=3，则S△ACD=（ ）
如图，在△ABC中，点D在边BC上，若∠BAD=∠CAD，AB=6，AC=3，S△ABD=3，则S△ACD=（ ）| A． | 3 | B． | 6 | C． | $\frac{3}{2}$ | D． | $\frac{9}{2}$ |
7．
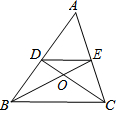如图，△ABC的两条中线BE、CD交于O，则S△EDO：S△ADE=（ ）
如图，△ABC的两条中线BE、CD交于O，则S△EDO：S△ADE=（ ）| A． | 1：2 | B． | 1：3 | C． | 1：4 | D． | 1：6 |
4．43表示的意义是（ ）
| A． | 4×3 | B． | 4个3相加 | C． | 4个3相乘 | D． | 3个4相乘 |
11．
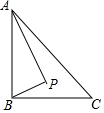如图，Rt△ABC中，AB⊥BC，AB=10，BC=12，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（ ）
如图，Rt△ABC中，AB⊥BC，AB=10，BC=12，P是△ABC内部的一个动点，且满足∠PAB=∠PBC，则线段CP长的最小值为（ ）| A． | 7 | B． | 8 | C． | $\frac{8\sqrt{13}}{13}$ | D． | $\frac{12\sqrt{13}}{13}$ |
9．下列各式，分解因式正确的是（ ）
| A． | a2-b2=（a-b）2 | B． | a2-2ab+b2-1=（a-b+1）（a-b-1） | ||
| C． | x3y-4xy=xy（x2-4） | D． | xy+xz+x=x（y+z） |