题目内容
 如图:D,E分别是△ABC的边BC,AC上的点,若∠B=∠C,∠ADE=∠AED,∠BAD=30°,则∠EDC=
如图:D,E分别是△ABC的边BC,AC上的点,若∠B=∠C,∠ADE=∠AED,∠BAD=30°,则∠EDC=考点:三角形内角和定理,三角形的外角性质
专题:
分析:先根据三角形外角的性质得出∠ADC=∠B+∠BAD=∠B+30°,∠AED=∠C+∠EDC,再根据∠B=∠C,∠ADE=∠AED即可得出结论.
解答:
解:∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠BAD=∠B+30°,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC,
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC-∠EDC=∠B+30°-∠EDC=∠B+∠EDC,
解得∠EDC=15°.
故答案为:15.
∴∠ADC=∠B+∠BAD=∠B+30°,
∵∠AED是△CDE的外角,
∴∠AED=∠C+∠EDC,
∵∠B=∠C,∠ADE=∠AED,
∴∠ADC-∠EDC=∠B+30°-∠EDC=∠B+∠EDC,
解得∠EDC=15°.
故答案为:15.
点评:本题考查的是三角形外角的性质,熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键.

练习册系列答案
相关题目
下列计算正确的是( )
| A、a2+a2=a4 |
| B、a2•a3=a6 |
| C、(ab3)2=ab6 |
| D、a3÷a2=a |
 如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAC=25°,则∠EAC的度数为( )
如图,△ABC≌△ADE,若∠B=80°,∠C=30°,∠DAC=25°,则∠EAC的度数为( )| A、40° | B、35° |
| C、30° | D、45° |
 如图,已知正方ABCD形的边长为1,连结AC、BD相交于O,E是OD的中点,求CE的长.
如图,已知正方ABCD形的边长为1,连结AC、BD相交于O,E是OD的中点,求CE的长.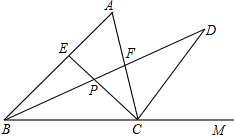 如图所示,在△ABC中∠A=60°,∠ABC的角平分线和∠ACB的外角平分线交于点D,与∠ACB的角平分线交于点P,与边AC交于点F.
如图所示,在△ABC中∠A=60°,∠ABC的角平分线和∠ACB的外角平分线交于点D,与∠ACB的角平分线交于点P,与边AC交于点F.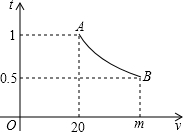 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=