题目内容
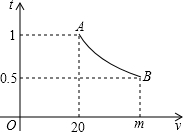 一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系:t=| k |
| v |
(1)求k和m的值;
(2)若行驶速度不得超过60km/h,则汽车通过该路段最少需要多少时间?
考点:反比例函数的应用
专题:
分析:(1)将点A(20,1)代入t=
,求得k,再把点B代入求出的解析式中,求得m的值;
(2)将v≤60代入(1)中所求的反比例函数解析式,解不等式即可求解.
| k |
| v |
(2)将v≤60代入(1)中所求的反比例函数解析式,解不等式即可求解.
解答:
解:(1)由题意得,函数t=
经过点A(20,1),
把(20,1)代入t=
,得k=20,
故可得:解析式为t=
,
再把B(m,0.5)代入t=
,得m=40;
(2)∵t=
,
∴v=
,
∴当v≤60时,
≤60,
解得得t≥
,
∴汽车通过该路段最少需要
小时.
| k |
| v |
把(20,1)代入t=
| k |
| v |
故可得:解析式为t=
| 20 |
| v |
再把B(m,0.5)代入t=
| 20 |
| v |
(2)∵t=
| 20 |
| v |
∴v=
| 20 |
| t |
∴当v≤60时,
| 20 |
| t |
解得得t≥
| 1 |
| 3 |
∴汽车通过该路段最少需要
| 1 |
| 3 |
点评:本题考查了反比例函数的应用.现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.

练习册系列答案
相关题目
如果x是16的算术平方根,则x为( )
| A、16 | B、4 | C、±4 | D、256 |
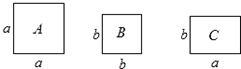 现有若干张卡片,分别是正方形卡片A、B和长方形卡片C,卡片大小如图所示.如果要拼一个长为(a+2b),宽为(a+b)的大长方形,则需要C类卡片张数为( )
现有若干张卡片,分别是正方形卡片A、B和长方形卡片C,卡片大小如图所示.如果要拼一个长为(a+2b),宽为(a+b)的大长方形,则需要C类卡片张数为( ) 如图:D,E分别是△ABC的边BC,AC上的点,若∠B=∠C,∠ADE=∠AED,∠BAD=30°,则∠EDC=
如图:D,E分别是△ABC的边BC,AC上的点,若∠B=∠C,∠ADE=∠AED,∠BAD=30°,则∠EDC=