题目内容
1.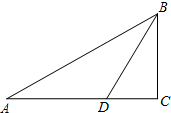 如图,在Rt△ABC中,∠C=90°,∠A=30°,如果D是AC上的点,且当AD=4时,∠BDC=45°,求BC的长.
如图,在Rt△ABC中,∠C=90°,∠A=30°,如果D是AC上的点,且当AD=4时,∠BDC=45°,求BC的长.
分析 设BC=x,由于昨天可知△BDC是等腰直角三角形,所以CD=BC=x,由含30度角的直角三角形的性质可知AB=2x,再利用勾股定理即可建立关于x的方程,解方程求出x的值即可.
解答 解:设BC=x,
∵在Rt△ABC中,∠C=90°,∠BDC=45°,
∴∠DBC=45°,
∴CD=BC=x,
∴AC=AD+CD=4+x,
∵∠A=30°,
∴AB=2x,
∴(2x)2=x2+(x+4)2,
解得:x=2$\sqrt{3}$+2或-2$\sqrt{3}$+2(舍),
即BC的长是2$\sqrt{3}$+2.
点评 本题主要考查了勾股定理的运用、等腰直角三角形的性质以及含30度角的直角三角形的性质,熟记勾股定理是解题的关键.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
11.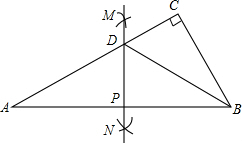 如图,△ABC中,∠C=90°,∠A=30°.分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.下列结论中,错误的是( )
如图,△ABC中,∠C=90°,∠A=30°.分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.下列结论中,错误的是( )
 如图,△ABC中,∠C=90°,∠A=30°.分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.下列结论中,错误的是( )
如图,△ABC中,∠C=90°,∠A=30°.分别以顶点A、B为圆心,大于$\frac{1}{2}$AB为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.下列结论中,错误的是( )| A. | 直线AB是线段MN的垂直平分线 | B. | CD=$\frac{1}{2}$AD | ||
| C. | BD平分∠ABC | D. | S△APD=S△BCD |
9.安定区某企业2014年的产值是360万元,要使2016年的产值达到490万元,设该企业这两年的平均增长率为x,根据题意列方程,则下列方程正确的是( )
| A. | 360x2=490 | B. | 360(1-x)2=490 | C. | 490(1+x)2=360 | D. | 360(1+x)2=490 |
6.已知9m÷32m+2=$(\frac{1}{3})$n,n的值是( )
| A. | -2 | B. | 2 | C. | 0.5 | D. | -0.5 |
13.下列各数是4的平方根的是( )
| A. | ±2 | B. | 2 | C. | -2 | D. | $\sqrt{2}$ |



