题目内容
11.某电脑城要用80000元的资金购进A,B两种型号的电脑25台,已知A型电脑进价为4000元,可以卖到4800元,B型电脑进价为2500元可以卖到3500元,根据以往的销售经验,A型电脑的购进不能低于8台.(1)请问电脑城有几种购进方案?
(2)哪种进货方案利润最大?最大利润是多少?
分析 (1)根据电脑城要用80000元的资金购进A,B两种型号的电脑25台,结合电脑的价格得出不等关系求出即可;
(2)利用题意可得:A型号电脑进的越少,B型号电脑进的越多时利润就越大,进而求出最大利润.
解答 解:(1)设购进A型号的电脑x台,那么购进B型号的电脑(25-x)台,根据题意得:
4000x+2500(25-x)≤80000,
解得:x≤11$\frac{2}{3}$,
∵A型号的电脑购进不能低于8台,
∴8≤x≤11$\frac{2}{3}$,
∴电脑城有4种购进电脑的方案:
①A型号购进8台时B型号购进17台
②A型号购进9台时B型号购进16台
③A型号购进10台时B型号购进15台
④A型号购进11台时B型号购进14台.
(2)∵A型号电脑的利润低,∴A型号电脑进的越少,B型号电脑进的越多时利润就越大,
∴按方案①进货利润最大.
最大利润为:8×800+17×1000=23400(元).
点评 此题主要考查了一元一次不等式的应用,根据题意表示出购买电脑的费用是解题关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
19.若a<b<0,则下列结论中错误的是( )
| A. | b-a>0 | B. | $\frac{a}{b}$>1 | C. | a-3<b-3 | D. | 5-a<5-b |
3.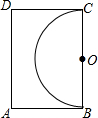 如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
 如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )
如图,王大伯家屋后有一块长12m,宽8m的矩形空地,他在以长边BC为直径的半圆内种菜,他家养的一只羊平时拴在A处的一棵树上,为了不让羊吃到菜,拴羊的绳长可以选用( )| A. | 9m | B. | 7m | C. | 5m | D. | 3m |
20.以下问题,不适合用全面调查的是( )
| A. | 了解一批灯泡的使用寿命 | B. | 学校招聘教师,对应聘人员的面试 | ||
| C. | 了解全校学生的课外读书时间 | D. | 旅客上飞机前的安检 |
 如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D. 如图,∠ABD=125°,∠A=50°,则∠ACE的度数是105°.
如图,∠ABD=125°,∠A=50°,则∠ACE的度数是105°. 已知:如图所示的网格中,△ABC的顶点A的坐标为(0,5).
已知:如图所示的网格中,△ABC的顶点A的坐标为(0,5).