题目内容
4．不透明袋子中装有2个红球，1个白球和1个黑球，这些球除颜色外无其他差别，随机摸出1个球不放回，再随机摸出1个球，求两次均摸到红球的概率．分析 利用树状图得出所有符合题意的情况，进而理概率公式求出即可．
解答 解：如图所示：
，
所有的可能有12种，符合题意的有2种，故两次均摸到红球的概率为：$\frac{2}{12}$=$\frac{1}{6}$．
点评 此题主要考查了树状图法求概率，根据题意利用树状图得出所有情况是解题关键．
练习册系列答案
相关题目
12．在0、2、-1、-2这四个数中，最小的数为（ ）
| A． | 0 | B． | 2 | C． | -1 | D． | -2 |
9．
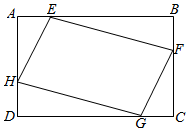如图，矩形ABCD中，AB=10，BC=5，点E，F，G，H分别在矩形ABCD各边上，且AE=CG，BF=DH，则四边形EFGH周长的最小值为（ ）
如图，矩形ABCD中，AB=10，BC=5，点E，F，G，H分别在矩形ABCD各边上，且AE=CG，BF=DH，则四边形EFGH周长的最小值为（ ）| A． | 5$\sqrt{5}$ | B． | 10$\sqrt{5}$ | C． | 10$\sqrt{3}$ | D． | 15$\sqrt{3}$ |
4．下列函数中，满足y的值随x的值增大而增大的是（ ）
| A． | y=3x-1 | B． | y=-2x | C． | y=$\frac{1}{x}$ | D． | y=x2 |