Question

3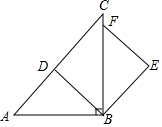．如图，等腰△ABC中，∠ABC=90°，点D在AC上，线段BD绕点B顺时针旋转90度到BE，EF∥DB交BC于点F．
（1）求证：△ABD≌△FBE．
（2）求证：BD⊥AC．

Answer 1

分析 （1）由旋转可求得BD=BE，∠DBE=90°，再结合条件AB=CB可判定△ABD≌△FBE；
（2）根据全等三角形的对应角相等，可得∠E=∠ADB，再根据EF∥DB，求得∠E=90°，即可得出BD⊥AC．

解答 证明：（1）由旋转可得，BD=BE，∠DBE=90°，
∴∠EBF+∠DBC=90°，
∵∠ABC=90°，
∴∠DBC+∠ABD=90°，
∴∠ABD=∠FBE，
在△ABD和△FBE中，
$\left\{\begin{array}{l}{AB=CB}\\{∠ABD=∠FBE}\\{DB=EB}\end{array}\right.$，
∴△ABD≌△FBE（SAS）；

（2）∵△ABD≌△FBE，
∴∠E=∠ADB，
∵EF∥BD，∠DBE=90°，
∴∠E=90°，
∴∠ADB=90°，
∴BD⊥AC．

点评 本题主要考查了旋转的性质以及全等三角形的判定和性质的综合运用，解决问题的关键是掌握：两边及其夹角分别对应相等的两个三角形全等；全等三角形的对应角相等．解题时注意：在图形旋转过程中，对应点到旋转中心的距离相等，对应点与旋转中心所连线段的夹角等于旋转角．