题目内容
14．圆的内接四边形ABCD的四个内角之比∠A：∠B：∠C：∠D的比值可能为（ ）| A． | 1：2：3：4 | B． | 1：4：3：2 | C． | 2：1：3：4 | D． | 1：2：1：2 |
分析 由四边形ABCD是圆内接四边形，根据圆的内接四边形的对角互补，可得∠A+∠C=∠B+∠D=180°，继而求得答案．
解答 解：∵四边形ABCD是圆内接四边形，
∴∠A+∠C=∠B+∠D=180°．
∴圆内接四边形ABCD的四个内角之比可能是：2：1：3：4．
故选C．
点评 此题考查了圆的内接多边形的性质，此题比较简单，注意圆的内接四边形的对角互补定理的应用是解此题的关键．
练习册系列答案
相关题目
2．
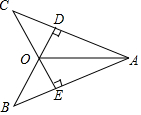如图，已知AB=AC，BD⊥AC于D，CE⊥AB于E，图中全等三角形的组数是（ ）
如图，已知AB=AC，BD⊥AC于D，CE⊥AB于E，图中全等三角形的组数是（ ）| A． | 5 | B． | 4 | C． | 3 | D． | 2 |
9．对于-3.$\stackrel{•}{2}$7$\stackrel{•}{1}$，下列说法不正确的是（ ）
| A． | 是负数 | B． | 是分数 | C． | 是有理数 | D． | 是无理数 |
19．下列各数：3.141 59，4.21，π，$\frac{22}{7}$，1.010 010 001…中，无理数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
6．两个相似三角形的相似比为9：5，则它们的面积比为（ ）
| A． | 9：5 | B． | 81：25 | C． | 3：$\sqrt{5}$ | D． | 不能确定 |
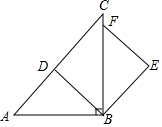如图，等腰△ABC中，∠ABC=90°，点D在AC上，线段BD绕点B顺时针旋转90度到BE，EF∥DB交BC于点F．