题目内容
18．
如图，△ABC中，∠ACB=90°，AC=24，BC=7，点M，N在AB上，且AM=AC，BN=BC，则MN的长为（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
分析 在直角三角形ABC中，由AC与BC的长，利用勾股定理求出AB的长，根据AM+BN-AB表示出MN的长，由AM=AC，NB=BC，等量代换后，将各自的值代入即可求出MN的长．
解答 解：∵在△ABC中，∠ACB=90°，AC=24，CB=7，
∴根据勾股定理得：AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=25，
又AM=AC，BN=BC，
则MN=AM+BN-AB=AC+BC-AB=24+7-25=6．
故选C．
点评 此题考查了勾股定理，利用了等量代换的思想，熟练掌握勾股定理是解本题的关键．
练习册系列答案
相关题目
8．一个数a在数轴上的对应点在原点左边，且|a|=9，则a的值为（ ）
| A． | 9或-9 | B． | 9 | C． | -9 | D． | 以上都不对 |
9．对于-3.$\stackrel{•}{2}$7$\stackrel{•}{1}$，下列说法不正确的是（ ）
| A． | 是负数 | B． | 是分数 | C． | 是有理数 | D． | 是无理数 |
6．两个相似三角形的相似比为9：5，则它们的面积比为（ ）
| A． | 9：5 | B． | 81：25 | C． | 3：$\sqrt{5}$ | D． | 不能确定 |
13．如果一个数的绝对值是它的相反数，则这个数是（ ）
| A． | 正数 | B． | 负数 | C． | 正数或零 | D． | 负数或零 |
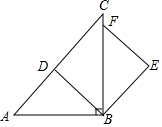如图，等腰△ABC中，∠ABC=90°，点D在AC上，线段BD绕点B顺时针旋转90度到BE，EF∥DB交BC于点F．
7．
用直尺和圆规作一个角等于已知角，如图，能得出∠O=∠O'的依据是（ ）
用直尺和圆规作一个角等于已知角，如图，能得出∠O=∠O'的依据是（ ）| A． | SAS | B． | ASA | C． | SSS | D． | AAS |