题目内容
13. 如图,方格纸中的每个小方格都是边长为1的正方形,在平面直角坐标系中,A(4,0),B(4,4),C(0,4)
如图,方格纸中的每个小方格都是边长为1的正方形,在平面直角坐标系中,A(4,0),B(4,4),C(0,4)(1)⊙M是△ABC的外接圆,则圆心M的坐标为(2,2).
(2)画出将△ABC绕原点O按逆时针方向旋转90°所得的△A1B1C1.
(3)若点P(m,n),且m+n=4,试分析当m分别取何值时,点P分别在⊙M外在⊙M上、在⊙M内?
分析 (1)根据点的坐标得出四边形ABCO是正方形,根据正方形的性质和点的坐标求出即可;
(2)根据旋转的性质找出各个对称点,连接即可得出三角形;
(3)求出P在直线AC上,根据A、C的坐标和点与圆的位置关系得出即可.
解答 解:(1)∵A(4,0),B(4,4),C(0,4),O(0,0),
∴BC=OC=OA=AB,∠COA=90°,
∴四边形ABCO是正方形,
∴M在AC和OB的交点上,
即M的坐标为(2,2),
故答案为:(2,2);
(2)如图所示,△A1B1C1即为所求;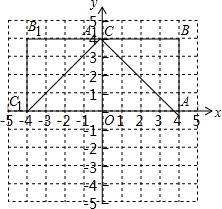
(3)∵点P(m,n),且m+n=4,
∴点P在直线y=-x+4上,即点P在直线AC上,
当m=0或m=4时,点P在⊙M上
当0<m<4时,点P在⊙M内;
当m<0或m>4时,点P在⊙M外.
点评 本题考查了正方形的性质和判定,旋转的性质,直线的解析式,点和圆的位置关系的应用,能综合运用知识点进行推理和计算是解此题的关键,综合性比较强,难度偏大.

练习册系列答案
相关题目
3.下列命题中是假命题的是( )
| A. | 三角形的外角等于与它不相邻的两个内角的和 | |
| B. | 有一个角为60°的等腰三角形是等边三角形 | |
| C. | 线段垂直平分线上的点到线段两端的距离相等 | |
| D. | 等腰三角形的中线与高重合 |
4.如图在表中填在各正方形中的四个数之间都有相同的规律,根据此规律,m的值是( )


| A. | 74 | B. | 104 | C. | 126 | D. | 144 |
 如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值.
如图,在四边形ABCD中,BC、AD不平行,且∠BAD+∠ADC=270°,E、F分别是AD、BC的中点,已知EF=4,求AB2+CD2的值. 从一副扑克牌中取出的两组牌如图所示,第一组牌是红桃1,2,3,第二组牌是方块1,2,3.将它们分别重新洗匀后,背面朝上放置,再从每组牌中各随机抽取1张.用画树状图(或列表)求抽出的两张牌的牌面数字之和是4的概率.
从一副扑克牌中取出的两组牌如图所示,第一组牌是红桃1,2,3,第二组牌是方块1,2,3.将它们分别重新洗匀后,背面朝上放置,再从每组牌中各随机抽取1张.用画树状图(或列表)求抽出的两张牌的牌面数字之和是4的概率.