Question

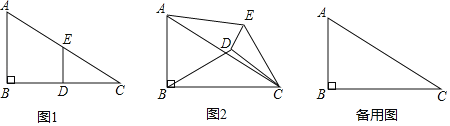
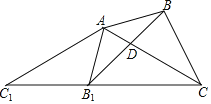
【题目】如图，△ABC中，∠BAC＝45°，∠ACB＝30°，将△ABC绕点A顺时针旋转得到△AB1C1，当点C1、B1、C三点共线时，旋转角为α，连接BB1，交AC于点D．下列结论：①△AC1C为等腰三角形；②△AB1D∽△BCD；③α＝75°；④CA＝CB1，其中正确的是（　　）

A.①③④B.①②④C.②③④D.①②③④

Answer 1

【答案】B

【解析】

将△ABC绕点A顺时针旋转得到△AB1C1，得到△ABC≌△AB1C1，根据全等三角形的性质得到AC1=AC，于是得到△AC1C为等腰三角形；故①正确；根据等腰三角形的性质得到∠C1=∠ACC1=30°，由三角形的内角和得到∠C1AC=120°，得到∠B1AB=120°，根据等腰三角形的性质得到∠AB1B=30°=∠ACB，于是得到△AB1D∽△BCD；故②正确；由旋转角α=120°，故③错误；根据旋转的性质得到∠C1AB1=∠BAC=45°，推出∠B1AC=∠AB1C，于是得到CA=CB1；故④正确．

解：∵将△ABC绕点A顺时针旋转得到△AB1C1，

∴△ABC≌△AB1C1，

∴AC1＝AC，

∴△AC1C为等腰三角形；故①正确；

∴AC1＝AC，

∴∠C1＝∠ACC1＝30°，

∴∠C1AC＝120°，

∴∠B1AB＝120°，

∵AB1＝AB，

∴∠AB1B＝30°＝∠ACB，

∵∠ADB1＝∠BDC，

∴△AB1D∽△BCD；故②正确；

∵旋转角为α，

∴α＝120°，故③错误；

∵∠C1AB1＝∠BAC＝45°，

∴∠B1AC＝75°，

∵∠AB1C1＝∠BAC＝105°，

∴∠AB1C＝75°，

∴∠B1AC＝∠AB1C，

∴CA＝CB1；故④正确．

故选：B．