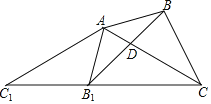
题目内容
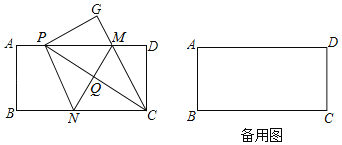
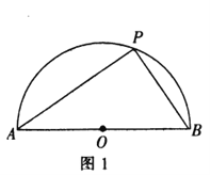
【题目】[问题发现]如图1,半圆![]() 的直径
的直径![]() 是半圆
是半圆![]() 上的一个动点,则
上的一个动点,则![]() 面积的最大值是_.
面积的最大值是_.
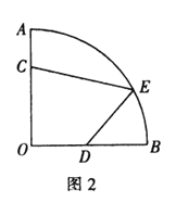
[问题解决]如图2所示的是某街心花园的一角.在扇形![]() 中,
中,![]() 米,在围墙
米,在围墙![]() 和
和![]() 上分别有两个入口
上分别有两个入口![]() 和
和![]() 且
且![]() 米,
米,![]() 是
是![]() 的中点,出口
的中点,出口![]() 在
在![]() 上.现准备沿
上.现准备沿![]() 从入口到出口铺设两条景观小路,在四边形
从入口到出口铺设两条景观小路,在四边形![]() 内种花,在剩余区域种草.
内种花,在剩余区域种草.
①出口![]() 设在距直线
设在距直线![]() 多远处可以使四边形
多远处可以使四边形![]() 的面积最大?最大面积是多少?(小路宽度不计)
的面积最大?最大面积是多少?(小路宽度不计)
②已知铺设小路![]() 所用的普通石材每米的造价是
所用的普通石材每米的造价是![]() 元,铺设小路
元,铺设小路![]() 所用的景观石材每米的造价是
所用的景观石材每米的造价是![]() 元问:在
元问:在![]() 上是否存在点
上是否存在点![]() ,使铺设小路
,使铺设小路![]() 和
和![]() 的总造价最低?若存在,请求出最低总造价和出口
的总造价最低?若存在,请求出最低总造价和出口![]() 距直线
距直线![]() 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
【答案】[问题发现]25;[问题解决]①出口![]() 设在距直线
设在距直线![]() 米处可以使四边形
米处可以使四边形![]() 的面积最大,最大为
的面积最大,最大为![]() 平方米;②总造价的最小值为
平方米;②总造价的最小值为![]() 元,出口
元,出口![]() 距直线
距直线![]() 的距离为
的距离为![]() 米
米
【解析】
[问题发现]![]() 的底边一定,面积最大也就是P点到AB的距离最大,故当
的底边一定,面积最大也就是P点到AB的距离最大,故当![]() 时底边
时底边![]() 上的高最大,再计算此时
上的高最大,再计算此时![]() 面积即可.
面积即可.
[问题解决]①根据四边形CODE面积=![]() ,求出
,求出![]() 最大时即可,然后作
最大时即可,然后作![]() ,证明
,证明![]() ,利用相似三角形的性质求出
,利用相似三角形的性质求出![]() 即可;
即可;
②先利用相似三角形将费用问题转化为CE+2DE=CE+QE,求CE+QE的最小值问题,然后利用相似三角形性质和勾股定理求解即可.
解:[问题发现]:
如图1,点![]() 运动至半圆
运动至半圆![]() 的中点时,底边
的中点时,底边![]() 上的高最大,即
上的高最大,即![]()
此时![]() 的面积最大,最大值为
的面积最大,最大值为![]() ;
;
[问题解决]![]() 如图2,连接
如图2,连接![]() 作
作![]() ,垂足为
,垂足为![]() 延长
延长![]() 交
交![]() 于点
于点![]() ,
,
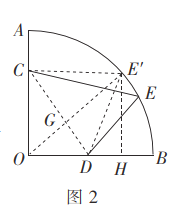
则此时![]() 的面积最大.
的面积最大.
![]() 为
为![]() 的中点,
的中点,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() 四边形
四边形![]() 面积的最大值为
面积的最大值为![]() ,
,
作![]() 垂足为
垂足为![]() ,
,
![]()
![]() .
.
又![]() ,
,
![]() ,
,
![]()
![]()
![]() ,
,
![]() 出口
出口![]() 设在距直线
设在距直线![]() 米处可以使四边形
米处可以使四边形![]() 的面积最大,最大为
的面积最大,最大为![]() 平方米;
平方米;
![]() 铺设小路
铺设小路![]() 和
和![]() 的总造价为
的总造价为![]()
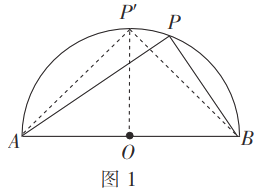
如图3,连接![]() 延长
延长![]() 到点
到点![]() 使
使![]() ,连接
,连接![]()
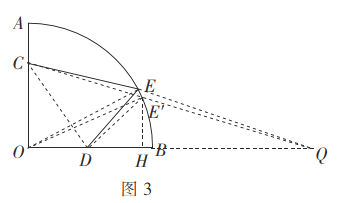
在![]() 与
与![]() 中,
中,![]() ,且
,且![]() ,
,
![]()
故![]()
![]() ,问题转化为求
,问题转化为求![]() 的最小值,
的最小值,
连接![]() 交
交![]() 于点
于点![]() ,
,
此时![]() 取得最小值为
取得最小值为![]() .
.
在![]() 中,
中,![]() ,
,
![]() ,
,
故总造价的最小值为![]() 元,
元,
作![]() 垂足为
垂足为![]() ,连接
,连接![]() .
.
设![]() 则
则![]() .
.
在![]() 中,
中,![]() ,
,
![]()
解得![]() ,
,![]() (舍去),
(舍去),
![]() 总造价的最小值为
总造价的最小值为![]() 元,出口
元,出口![]() 距直线
距直线![]() 的距离为
的距离为![]() 米.
米.

 全能练考卷系列答案
全能练考卷系列答案【题目】某校开展主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,学生会随机抽取了20名七、八年级学生(每个年级各10人)进行问卷调查,并把他们的得分绘制成了如下表格,计分采用10分制(得分均取整数)成绩达到6分或6分以上为及格,达到9分及以上为优秀,成绩如表1所示,并制作了成绩分析表(表2).
表1
七年级 | 5 | 8 | 8 |
| 8 | 10 | 10 | 8 | 5 | 5 |
八年级 | 10 | 6 | 6 | 9 |
| 4 | 5 | 7 | 10 | 8 |
表2
年级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
七年级 | 7.6 | 8 | 8 | 3.82 | 70% |
|
八年级 | 7.5 |
| 10 | 4.94 | 80% | 40% |
(1)在表1中,![]() _____,
_____,![]() _____;在表2中,
_____;在表2中,![]() _____,
_____,![]() ______;
______;
(2)根据表2成绩数据分析,你认为哪个年级的学生对垃圾分类了解更加深入,请说明你的理由;
(3)小明根据表2数据作出如下判断:
①七年级学生成绩的平均数高于八年级,故七年级学生一定比八年级学生优秀;
②被调查对象中,七年级学生的成绩更加稳定;
③学校七年级和八年级共有400人,估计有280人成绩达到优秀;
④七年级不及格人数比八年级多;
对小明的四个结论,随机任选两个,求都是错误的概率.