题目内容
11.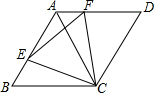 如图,菱形ABCD,∠B=60°,点E、F分别在AB、AD上,且BE=AF.求∠ECF的度数.
如图,菱形ABCD,∠B=60°,点E、F分别在AB、AD上,且BE=AF.求∠ECF的度数.
分析 由菱形ABCD,∠B=60°,易证得△ABC与△ACD是等边三角形,即可得AC=BC,∠DAC=°,又由BE=AF,即可证得△ACF≌△BCE,继而求得∠ECF=∠ACB=60°.
解答 解:∵四边形ABCD是菱形,
∴AB=BC,AD∥BC,
∵∠B=60°,
∴△ABC是等边三角形,
∴BC=AC,
∴∠ACB=∠B=60°,
∵AD∥BC,
∴∠DAC=∠ACB=60°,
∴∠DAC=∠B,
又∵AF=BE,
在△ACF和△BCE中,
$\left\{\begin{array}{l}{AF=BE}\\{∠CAF=∠B}\\{AC=BC}\end{array}\right.$,
∴△ACF≌△BCE(SAS),
∴∠ACF=∠BCE,
∴∠ECF=∠ACB=60°.
点评 此题考查了菱形的性质、等边三角形的判定与性质以及全等三角形的判定与性质.注意证得△ABC与△ACD是等边三角形,△ACF≌△BCE是解此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.某商品的进价为150元,售价为165元,则销售该商品的利润率为( )
| A. | 10% | B. | 9% | C. | 15元 | D. | 15% |
1.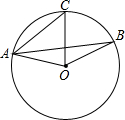 如图,在⊙O中,∠BAC=25°,则∠BOC的度数为( )
如图,在⊙O中,∠BAC=25°,则∠BOC的度数为( )
 如图,在⊙O中,∠BAC=25°,则∠BOC的度数为( )
如图,在⊙O中,∠BAC=25°,则∠BOC的度数为( )| A. | 25° | B. | 50° | C. | 60° | D. | 80° |
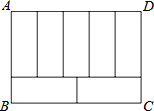 如图:周长为68的长方形ABCD被分成7个形状、大小完全一样的长方形,则ABCD的面积是多少?
如图:周长为68的长方形ABCD被分成7个形状、大小完全一样的长方形,则ABCD的面积是多少?