题目内容
7.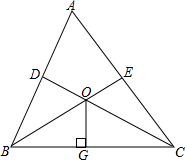 如图,△ABC中,∠BAC=60°,点D、E分别在AB、AC上,∠BCD=∠CBE=30°,BE、CD相交于点O,OG⊥BC于点G,求证:OE+OD=2OG.
如图,△ABC中,∠BAC=60°,点D、E分别在AB、AC上,∠BCD=∠CBE=30°,BE、CD相交于点O,OG⊥BC于点G,求证:OE+OD=2OG.
分析 延长OE至点M,使OM=OC,连接CM,由于∠BCD=∠CBE=30°,于是得到OB=OC,∠MOC=30°+30°=60°,推出△OMC为等边三角形,根据等边三角形的性质得到CM=OC=OB,∠M=60°,于是得到∠DBO=∠MCE,推出△BOD≌△MCE,根据全等三角形的性质得到DO=EM,证得OE+OD=OM=OB,根据直角三角形的性质得到2OG=OB,即可得到结论.
解答 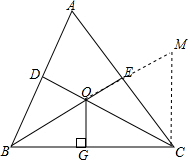 证明:延长OE至点M,使OM=OC,连接CM,
证明:延长OE至点M,使OM=OC,连接CM,
∵∠BCD=∠CBE=30°,
∴OB=OC,∠MOC=30°+30°=60°,
∵OM=OC,
∴△OMC为等边三角形,
∴CM=OC=OB,∠M=60°,
∴∠DBO=∠MCE,
在△BOD和△CME中,
$\left\{\begin{array}{l}{∠DBO=∠MCE}\\{BO=CM}\\{∠DOB=∠M}\end{array}\right.$,
∴△BOD≌△MCE,
∴DO=EM,
∴OE+OD=OM=OB,
在Rt△OBG中,∠OBG=30°,OG⊥BC,
∴2OG=OB,
∴OE+OD=2OG.
点评 本题考查了等边三角形的判定和性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
17.关于x的方程(x+1)2=4x根的情况叙述正确的一项是( )
| A. | 方程有两个不相等的实数根 | B. | 方程有增根 | ||
| C. | 方程有两个相等的根 | D. | 无解 |
17.已知实数x=4,y=8,则以x,y的值为两边长的等腰三角形的周长是( )
| A. | 20 | B. | 16 | C. | 20或16 | D. | 以上答案均不对 |
 如图,点B,E,F,C在一条直线上,AB=DC,BE=CF,∠B=∠C.求证:∠A=∠D.
如图,点B,E,F,C在一条直线上,AB=DC,BE=CF,∠B=∠C.求证:∠A=∠D.
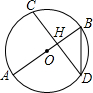 如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=2$\sqrt{2}$,BD=$\sqrt{3}$,则BH的长为( )
如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=2$\sqrt{2}$,BD=$\sqrt{3}$,则BH的长为( )