题目内容
如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△E1B2D2的面积为S1,△E2B3D3的面积为S2,…,△EnBn+1Dn+1的面积为Sn,则S1= ,Sn= .


考点:相似三角形的判定与性质,等边三角形的性质
专题:规律型
分析:根据等边三角形的性质求出等边三角形的高,连接B1Bn+1,可得B1Bn+1为n个边长为2的等边三角形的一边所在的直线,然后根据相似三角形对应边成比例求出
,B2D2,再根据等边三角形的性质求出点E1到B2D2的距离,然后利用三角形的面积公式求出S1,依此类推求出EnBn+1、Bn+1Dn+1,再求出点En到Bn+1Dn+1的距离,然后根据三角形的面积公式列式计算即可得解.
| E1B2 |
| B2C1 |
解答: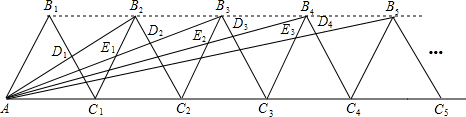 解:∵等边三角形的边长为2,
解:∵等边三角形的边长为2,
∴等边三角形的高为2×
=
,
如图,连接B1Bn+1,则B1Bn+1为n个边长为2的等边三角形的一边所在的直线,
∴B1Bn+1∥ACn,
∴△AC1E1∽△B3B2E1,△AC2D2∽△B3B2D2,
∴
=
=
=1,
=
=
=
,
∴
=
=
,B2D2=2×
=
,
∴点E1到B2D2的距离=
×
=
,
∴S1=
B2D2•
=
•
•
=
;
同理可求,点E2到B3D3的距离=
×
=
,
…,
点En到Bn+1Dn+1的距离=
×
=
,
B3D3=2×
=
,
…,
Bn+1Dn+1=2×
=
,
∴Sn=
•
•
=
.
故答案为:
;
.
 解:∵等边三角形的边长为2,
解:∵等边三角形的边长为2,∴等边三角形的高为2×
| ||
| 2 |
| 3 |
如图,连接B1Bn+1,则B1Bn+1为n个边长为2的等边三角形的一边所在的直线,
∴B1Bn+1∥ACn,
∴△AC1E1∽△B3B2E1,△AC2D2∽△B3B2D2,
∴
| E1B2 |
| E1C1 |
| B3B2 |
| AC1 |
| 2 |
| 2 |
| B2D2 |
| C2D2 |
| B3B2 |
| AC2 |
| 2 |
| 4 |
| 1 |
| 2 |
∴
| E1B2 |
| B2C1 |
| 1 |
| 1+1 |
| 1 |
| 2 |
| 1 |
| 1+2 |
| 2 |
| 3 |
∴点E1到B2D2的距离=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴S1=
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 6 |
同理可求,点E2到B3D3的距离=
| 1 |
| 1+2 |
| 3 |
| ||
| 3 |
…,
点En到Bn+1Dn+1的距离=
| 1 |
| n+1 |
| 3 |
| ||
| n+1 |
B3D3=2×
| 1 |
| 1+3 |
| 2 |
| 4 |
…,
Bn+1Dn+1=2×
| 1 |
| 1+(n+1) |
| 2 |
| n+2 |
∴Sn=
| 1 |
| 2 |
| 2 |
| n+2 |
| ||
| n+1 |
| ||
| (n+1)(n+2) |
故答案为:
| ||
| 6 |
| ||
| (n+1)(n+2) |
点评:本题考查了相似三角形的判定与性质,等边三角形的判定与性质,作辅助线得到平行线从而得到相似三角形是解题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
下列各式中计算正确的是( )
| A、a3+3a3=4a3 |
| B、a4-a=a3 |
| C、a3•a4=a12 |
| D、(a3)2÷a4=a |
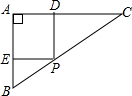 如图,Rt△ABC中,∠BAC=90°,AB=3,AC=4,P是BC上一点,作PE⊥AB于E,PD⊥AC于D.设BP=x,则PD+PE等于( )
如图,Rt△ABC中,∠BAC=90°,AB=3,AC=4,P是BC上一点,作PE⊥AB于E,PD⊥AC于D.设BP=x,则PD+PE等于( )A、4-
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知∠BAC,在AC边上有一点D,请利用尺规,过点D作BA的平行线(保留作图痕迹)
如图,已知∠BAC,在AC边上有一点D,请利用尺规,过点D作BA的平行线(保留作图痕迹)

 如图,四边形ABCD是平行四边形,AC是对角线,BE⊥AC,垂足为E;DF⊥AC,垂足为F.
如图,四边形ABCD是平行四边形,AC是对角线,BE⊥AC,垂足为E;DF⊥AC,垂足为F.