题目内容
14.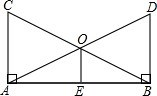 如图,∠BAC=∠ABD=90°,AC=BD,点O是AD,BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并说明理由.
如图,∠BAC=∠ABD=90°,AC=BD,点O是AD,BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并说明理由.
分析 由全等三角形的判定定理可得△ABC≌△BAD,利用全等三角形的性质可得∠CBA=∠DAB,∠C=∠D,由点E是AB的中点利用等腰三角形的性质可得结果.
解答 解:OE⊥AB,
理由:
在△ABC和△BAD中,
$\left\{\begin{array}{l}{AC=BD}\\{∠BAC=∠ABD}\\{AB=BA}\end{array}\right.$,
∴△ABC≌△BAD,
∴∠CBA=∠DAB,∠C=∠D,
∴OA=OB,
∵点E是AB的中点,
∴OE⊥AB.
点评 本题主要考查了三角形全等的判定及性质定理和等腰三角形的判定及性质定理,发现三角形全等的条件,运用等腰三角形“三线合一”是解答此题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
5.下列说法中,不正确的是( )
| A. | 所有的负分数都是有理数 | B. | 所有的正整数都是有理数 | ||
| C. | $\frac{5}{2}$是有理数 | D. | 0不是有理数 |
2.二次函数y=ax2+bx+c(a,b,c为常数,a<0)的图象经过点(-1,1),(4,-4).下列结论:
①$\frac{a}{c}$<0;
②当x>1时,y的值随x值的增大而减小;
③x=4是方程ax2+(b+1)x+c=0的一个根;
④当-1<x<4时,ax2+(b+1)x+c>0.
其中正确的是( )
①$\frac{a}{c}$<0;
②当x>1时,y的值随x值的增大而减小;
③x=4是方程ax2+(b+1)x+c=0的一个根;
④当-1<x<4时,ax2+(b+1)x+c>0.
其中正确的是( )
| A. | ①③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
9. 根据输入的有理数,按图中程序计算,并把输出的结果填入表内:
根据输入的有理数,按图中程序计算,并把输出的结果填入表内:
 根据输入的有理数,按图中程序计算,并把输出的结果填入表内:
根据输入的有理数,按图中程序计算,并把输出的结果填入表内:| 输入 | 输出 |
| 1 | 6 |
| -6 | 4 |
6.点(-2,5),(4,5)是抛物线y=ax2-bx+c上两点,则抛物线的对称轴是( )
| A. | 直线x=-a | B. | 直线x=1 | C. | 直线x=0 | D. | 直线x=3 |
4.下列结论不正确的是( )
| A. | 若a>0,b<0,且a>|b|,则a+b<0 | B. | 若a<0,b>0,且|a|>b,则a+b<0 | ||
| C. | 若a>0,b>0,则a+b>0 | D. | 若a<0,b<0,则a+b<0 |
 在平面直角坐标系xOy中,抛物线C1:y=mx2-2mx+m+4与y轴交于点A(0,3),与x轴交于点B、C(点B在点C左侧).
在平面直角坐标系xOy中,抛物线C1:y=mx2-2mx+m+4与y轴交于点A(0,3),与x轴交于点B、C(点B在点C左侧).