题目内容
12.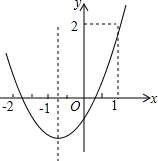 二次函数y=ax2+bx+c的图象如图所示,则下列说法:①abc<0;②2a>b;③a+c>1;④9a+c<3b+2,其中正确的个数是( )
二次函数y=ax2+bx+c的图象如图所示,则下列说法:①abc<0;②2a>b;③a+c>1;④9a+c<3b+2,其中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由抛物线开口方向得到a>0,由抛物线的对称轴为直线x=-$\frac{b}{2a}$>-1得到b<2a,由抛物线与y轴的交点在x轴下方得到c<0,所以abc<0;根据x=1时,y=2,x=-1时,y<0,确定a+c与1的关系,根据x=-3时,y>2,确定9a+c与3b+2的关系.
解答 解:∵抛物线开口向上,
∴a>0,
∵对称轴在y轴左侧,
∴b>0,
∵抛物线与y轴的交点在x轴下方,
∴c<0,
∴abc<0,①正确;
∵x=-$\frac{b}{2a}$>-1,
∴b<2a,②正确;
∵x=1时,y=2,
∴a+b+c=2,
∵x=-1时,y<0,
∴a-b+c<0,
∴2a+2c<2,
∴a+c<1,③错误;
∵对称轴为直线x=-$\frac{b}{2a}$>-1,
∴x=1关于对称轴的对称点在x=-3的右侧,
∴x=-3时,y>2,即9a-3b+c>2,
∴9a+c>3b+2,④错误.
故选:B.
点评 本题考查的是二次函数图形与系数的关系,二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线开口向上,当a<0时,抛物线开口向下;一次项系数b和二次项系数a共同决定对称轴的位置. 当a与b同号时,对称轴在y轴左; 当a与b异号时,对称轴在y轴右,常数项c决定抛物线与y轴交点.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
2.二次函数y=ax2+bx+c(a,b,c为常数,a<0)的图象经过点(-1,1),(4,-4).下列结论:
①$\frac{a}{c}$<0;
②当x>1时,y的值随x值的增大而减小;
③x=4是方程ax2+(b+1)x+c=0的一个根;
④当-1<x<4时,ax2+(b+1)x+c>0.
其中正确的是( )
①$\frac{a}{c}$<0;
②当x>1时,y的值随x值的增大而减小;
③x=4是方程ax2+(b+1)x+c=0的一个根;
④当-1<x<4时,ax2+(b+1)x+c>0.
其中正确的是( )
| A. | ①③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
4.下列结论不正确的是( )
| A. | 若a>0,b<0,且a>|b|,则a+b<0 | B. | 若a<0,b>0,且|a|>b,则a+b<0 | ||
| C. | 若a>0,b>0,则a+b>0 | D. | 若a<0,b<0,则a+b<0 |
2.某商店在一次买卖中,同时卖出两种货物,每种货物的售价均为960元.若按成本计算,一种货物盈利20%,另一种亏本20%,则这次交易商店( )
| A. | 赚160元 | B. | 赔80元 | C. | 赔240元 | D. | 赚400元 |
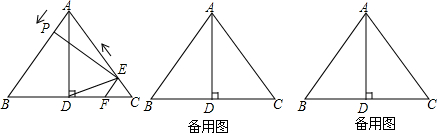
 如图,AD是△ABC的中线,延长AD到E,使DE=AD,连结BE,则有△ACD≌△EBD.
如图,AD是△ABC的中线,延长AD到E,使DE=AD,连结BE,则有△ACD≌△EBD.