题目内容
1. 如图,⊙O中,弦AB=2,点C在⊙O上,∠ACB=45°,则⊙O的半径等于( )
如图,⊙O中,弦AB=2,点C在⊙O上,∠ACB=45°,则⊙O的半径等于( )| A. | $\sqrt{2}$ | B. | 1 | C. | 2$\sqrt{2}$ | D. | 2 |
分析 过B点作直径AD,连AD,根据圆周角定理可得∠DAB=90°,∠D=∠C=45°,再根据三角形函数定义可得BD=$\sqrt{2}$AB=2$\sqrt{2}$,然后可得BO长.
解答  解:过B点作直径AD,连AD,如图,
解:过B点作直径AD,连AD,如图,
∴∠DAB=90°,∠D=∠C=45°,
∴△ABD为等腰直角三角形,
而AB=2,
∴BD=$\sqrt{2}$AB=2$\sqrt{2}$,
∴OB=$\sqrt{2}$.
故选:A.
点评 此题主要考查了圆周角定理,以及等腰直角三角形的性质,培养了学生分析问题、解决问题的能力.关键是正确作出辅助线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 已知:如图,AB是⊙O的直径,弦CD⊥AB,M为AC上一点,AM的延长线交DC的延长线于F,求证:∠AMD=∠FMC.
已知:如图,AB是⊙O的直径,弦CD⊥AB,M为AC上一点,AM的延长线交DC的延长线于F,求证:∠AMD=∠FMC.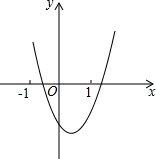 二次函数y=ax2+bx+c的图象如图所示,请写出一次函数y=bx+b2-4ac与反比例函数y=$\frac{a+b+c}{x}$的图象分别经过哪几个象限?并说明理由.
二次函数y=ax2+bx+c的图象如图所示,请写出一次函数y=bx+b2-4ac与反比例函数y=$\frac{a+b+c}{x}$的图象分别经过哪几个象限?并说明理由.