题目内容
9.解方程|x-1|+|x+2|=5.分析 分成x≤-2,-2<x≤1,x>1三种情况进行讨论,去掉绝对值符号求解.
解答 解:当x≤-2时,原式即1-x-x-2=5,
即-2x=6,
解得x=-3;
当-2<x≤1时,原式即1-x+x+2=5,无解;
当x>1时,原式即x-1+x+2=5,
解得x=2.
则x=-3或2.
点评 本题考查了函数绝对值的方程的解法,解题的关键是正确进行讨论,去掉绝对值符号.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
20.如图所示的长方形和正方形硬纸片,如果要用这些纸片若干个拼一个长为(3a+2b)宽为(a+b)的长方形,Ⅰ型、Ⅱ型、Ⅲ型纸片所需块数分别为( )


| A. | 3,5,2 | B. | 3,2,2 | C. | 2,3,5 | D. | 1,2,5 |
1. 如图,⊙O中,弦AB=2,点C在⊙O上,∠ACB=45°,则⊙O的半径等于( )
如图,⊙O中,弦AB=2,点C在⊙O上,∠ACB=45°,则⊙O的半径等于( )
 如图,⊙O中,弦AB=2,点C在⊙O上,∠ACB=45°,则⊙O的半径等于( )
如图,⊙O中,弦AB=2,点C在⊙O上,∠ACB=45°,则⊙O的半径等于( )| A. | $\sqrt{2}$ | B. | 1 | C. | 2$\sqrt{2}$ | D. | 2 |
 如图,直线y=$\frac{1}{2}$x+1交两坐标轴于A、B两点,P从O点出发.
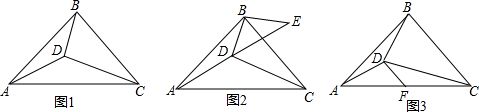
如图,直线y=$\frac{1}{2}$x+1交两坐标轴于A、B两点,P从O点出发. 已知三角形ABC的面积为96平方厘米,BC=3DC,FD=2AF,求三角形AEF的面积.
已知三角形ABC的面积为96平方厘米,BC=3DC,FD=2AF,求三角形AEF的面积.