题目内容
20.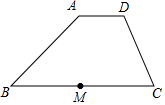 已知:如图,在梯形ABCD中,AD∥BC,AD=$\frac{1}{3}$BC,点M是边BC的中点,$\overrightarrow{AD}$=$\overrightarrow a$,$\overrightarrow{AB}$=$\overrightarrow b$.
已知:如图,在梯形ABCD中,AD∥BC,AD=$\frac{1}{3}$BC,点M是边BC的中点,$\overrightarrow{AD}$=$\overrightarrow a$,$\overrightarrow{AB}$=$\overrightarrow b$.(1)填空:$\overrightarrow{BM}$=$\frac{3}{2}$$\overrightarrow a$,$\overrightarrow{MA}$=-$\frac{3}{2}$$\overrightarrow a$-$\overrightarrow{b}$.(结果用$\overrightarrow a$、$\overrightarrow b$表示).
(2)直接在图中画出向量3$\overrightarrow a$+$\overrightarrow b$.(不要求写作法,但要指出图中表示结论的向量)
分析 (1)由在梯形ABCD中,AD∥BC,AD=$\frac{1}{3}$,可求得$\overrightarrow{BC}$,然后由点M是边BC的中点,求得$\overrightarrow{BM}$,再利用三角形法则求解即可求得$\overrightarrow{MA}$;
(2)利用三角形法则连结AC求解即可.
解答 解:(1)∵在梯形ABCD中,AD∥BC,AD=$\frac{1}{3}$BC,$\overrightarrow{AD}$=$\overrightarrow a$,
∴$\overrightarrow{BC}$=3$\overrightarrow{AD}$=3$\overrightarrow a$,
∵点M是边BC的中点,
∴$\overrightarrow{BM}$=$\frac{1}{2}$$\overrightarrow{BC}$=$\frac{3}{2}$$\overrightarrow a$;
∴$\overrightarrow{MA}$=-$\overrightarrow{AM}$=-($\overrightarrow{AB}$+$\overrightarrow{BM}$)=-$\frac{3}{2}$$\overrightarrow a$-$\overrightarrow{b}$;
故答案为:$\frac{3}{2}$$\overrightarrow a$;-$\frac{3}{2}$$\overrightarrow a$-$\overrightarrow{b}$;
(2)如图所示,连结AC,$\overrightarrow{AC}$就是所求作的向量.
点评 此题考查了平面向量的知识以及平行四边形的性质.注意掌握平行四边形法则与三角形法则的应用是解此题的关键.

?①(-24)÷(-8)=3;
?②36÷(-9)=4;?
③(-3)×4÷$\frac{1}{3}$=-4;
④(-5.25-2.25+6.25)×0=-1
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
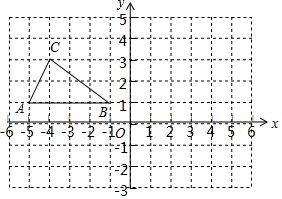 如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-5,1),B(-1,1),C(-4,3).
如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-5,1),B(-1,1),C(-4,3).