题目内容
8.如果关于字母x的二次多项式-3x2+mx+nx2-x+3的值与x的取值无关,求2m-3n的值.分析 先把多项式进行合并同类项得(n-3)x2+(m-1)x+3,由于关于字母x的二次多项式-3x2+mx+nx2-x+3的值与x无关,即不含x的项,所以n-3=0,m-1=0,然后解出m、n计算它们的和即可.
解答 解:合并同类项得(n-3)x2+(m-1)x+3,
根据题意得n-3=0,m-1=0,
解得m=1,n=3,
所以2m-3n=2-9=-7.
点评 本题考查了多项式:几个单项式的和叫做多项式,每个单项式叫做多项式的项,其中不含字母的项叫做常数项.多项式中次数最高的项的次数叫做多项式的次数.

练习册系列答案
相关题目
13.在-8,2.6,-3$\frac{1}{2}$,0,2$\frac{2}{3}$,-5.7中,负数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 5个 |
18.据2010年第六次全国人口普查公布的数据显示,全桂林市总人口为498.84万人,那么用科学记数法表示为( )人.
| A. | 4.98846 | B. | 4.9884×106 | C. | 4.9884×107 | D. | 4.9884×108 |
 如图是抛物线形拱桥,当水面在l时,拱顶离水面2m,水面宽4m,水面下降1m后,水面宽多少?
如图是抛物线形拱桥,当水面在l时,拱顶离水面2m,水面宽4m,水面下降1m后,水面宽多少?
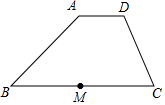 已知:如图,在梯形ABCD中,AD∥BC,AD=$\frac{1}{3}$BC,点M是边BC的中点,$\overrightarrow{AD}$=$\overrightarrow a$,$\overrightarrow{AB}$=$\overrightarrow b$.
已知:如图,在梯形ABCD中,AD∥BC,AD=$\frac{1}{3}$BC,点M是边BC的中点,$\overrightarrow{AD}$=$\overrightarrow a$,$\overrightarrow{AB}$=$\overrightarrow b$.