题目内容
20.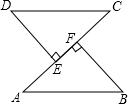 已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.
已知:如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.求证:(1)AE=CF;(2)AB∥CD.
分析 (1)利用HL定理即可证明△ABF≌△CDE,证明AF=CE,据此即可得到AE=CF;
(2)根据△ABF≌△CDE即可证得∠A=∠C,然后利用平行线的判定定理证明.
解答 证明:(1)∵DE⊥AC,BF⊥AC,
∴∠DEC=∠BFA=90°,
∴在RT△ABF和RT△CDE中,
$\left\{\begin{array}{l}{AB=CD}\\{DE=BF}\end{array}\right.$,
∴△ABF≌△CDE(HL);
∴AF=CE,
即AF-EF=CE-EF
∴AE=CF;
(2)∵△ABF≌△CDE,
∴∠A=∠C,
∴CD∥AB.
点评 本题考查了全等三角形的判定与性质以及平行线的判定,正确证明△ABF≌△CDE是关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
8.当ab<0时,y=ax2与y=ax+b的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
5.计算:(-3+4)的结果的相反数等于( )
| A. | 7 | B. | -7 | C. | 1 | D. | -1 |
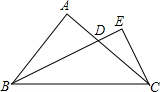 已知Rt△ABC,∠BAC=90°,AB=AC,过点B的直线BE交直线AC于D,CE⊥BE于E,当BE平分∠ABC,求证:①BD=2CE;②AB+AD=BC.
已知Rt△ABC,∠BAC=90°,AB=AC,过点B的直线BE交直线AC于D,CE⊥BE于E,当BE平分∠ABC,求证:①BD=2CE;②AB+AD=BC.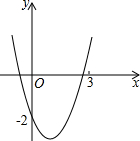 如图,已知抛物线y=x2+bx+c经过点(0,-2),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你所确定的b的值为-$\frac{7}{3}$<b<1.
如图,已知抛物线y=x2+bx+c经过点(0,-2),请你确定一个b的值,使该抛物线与x轴的一个交点在(1,0)和(3,0)之间.你所确定的b的值为-$\frac{7}{3}$<b<1.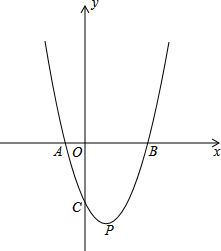 已知抛物线y=ax2-2ax+a-4与x轴分别交于A,B,与y轴交于C点,顶点为P.
已知抛物线y=ax2-2ax+a-4与x轴分别交于A,B,与y轴交于C点,顶点为P.