题目内容
4.计算:($\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{2015}$)×(1+$\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{2014}$)-(1+$\frac{1}{2}+\frac{1}{3}$+…+$\frac{1}{2015}$)×($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2014}$).分析 设1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2015}$=x,原式变形后计算即可得到结果.
解答 解:设1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2015}$=x,
原式=(x-1)(x-$\frac{1}{2015}$)-x(x-1-$\frac{1}{2015}$)
=x2-$\frac{1}{2015}$x-x+$\frac{1}{2015}$-x2+x+$\frac{1}{2015}$x
=$\frac{1}{2015}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
12.下列各式正确的是( )
| A. | x2-(2x-3y+4z)=x2-2x-3y-4z | B. | (a+2)-(-3b+c)=a+2+3b+c | ||
| C. | 3m-[5n-(2a-8)]=3m-5n+2a-8 | D. | x2-y2+z2=x2-(y2+z2-a2) |
9.下列说法错误的是( )
| A. | 两个面积相等的圆一定全等 | |
| B. | 全等三角形是指形状、大小都相同的三角形 | |
| C. | 底边相等的两个等腰三角形全等 | |
| D. | 斜边上中线和一条直角边对应相等的两直角三角形全等 |
13.已知等腰三角形的两边长分别为6cm、3cm,则该等腰三角形的周长是( )
| A. | 9cm | B. | 12cm | C. | 12cm或15cm | D. | 15cm |
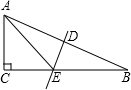 在△ABC中,DE垂直平分斜边AB,分别交AB、BC于D、E.
在△ABC中,DE垂直平分斜边AB,分别交AB、BC于D、E.