题目内容
13.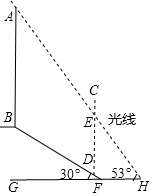 如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线AC与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为( )
如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线AC与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,$\sqrt{3}$≈1.73)
| A. | 35.5米 | B. | 37.6米 | C. | 38.6米 | D. | 40.3米 |
分析 作CG⊥AB、作BP⊥DE,在Rt△BDP中求得DP=15、PB=BDcos∠DBP=15$\sqrt{3}$,继而知PE=BG=4,在Rt△ACG中求得AG=$\frac{GE}{tan∠EAG}$=$\frac{15\sqrt{3}}{tan37°}$,根据AB=AG+BG得出答案.
解答 解:如图,作CG⊥AB于点G,作BP⊥DE于点P,
则∠DBP=∠BFG=30°,
∵BD=30,
∴DP=$\frac{1}{2}$BD=15,BP=BDcos∠DBP=30×$\frac{\sqrt{3}}{2}$=15$\sqrt{3}$,
∵DE=19,
∴PE=BG=DE-DP=4,
∵∠AEG=∠H=53°,
∴∠EAG=37°
∴AG=$\frac{GE}{tan∠EAG}$=$\frac{15\sqrt{3}}{tan37°}$,
则AB=AG+BG=$\frac{15\sqrt{3}}{tan37°}$+4≈38.6,
故选:C.
点评 本题考查了解直角三角形的应用,解答本题的根据题目所给的坡角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
相关题目
4.下列各式中从左到右的变形属于因式分解的是( )
| A. | a(a+b-1)=a2+ab-a | B. | a2-a-2=(a-1)-2 | ||
| C. | 4a2-9b2=(2a-3b)(2a+3b) | D. | a2-4+3a=(a+2)(a-2)+3a |
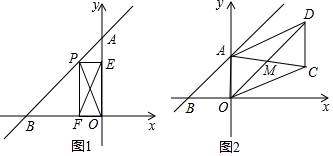

 在网格中仅利用没有刻度的直尺画图:
在网格中仅利用没有刻度的直尺画图: