题目内容
8.解分式方程:$\frac{3-x}{x-4}$+$\frac{2}{4-x}$=2.分析 观察可得最简公分母是(x-4),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
解答 解:$\frac{3-x}{x-4}$+$\frac{2}{4-x}$=2,
3-x-2=2(x-4),
3-x-2=2x-8,
-x-2x=-8-3+2,
-3x=-9,
x=3,
检验:当x=3时,x-4≠0,
故原分式方程的解是x=3.
点评 考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
16.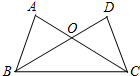 如图,AC,BD交于点O,∠ABC=∠DCB,下列条件中不能判定△ABC≌△DCB的是( )
如图,AC,BD交于点O,∠ABC=∠DCB,下列条件中不能判定△ABC≌△DCB的是( )
 如图,AC,BD交于点O,∠ABC=∠DCB,下列条件中不能判定△ABC≌△DCB的是( )
如图,AC,BD交于点O,∠ABC=∠DCB,下列条件中不能判定△ABC≌△DCB的是( )| A. | ∠ACB=∠DBC | B. | AC=DB | C. | AB=DC | D. | ∠A=∠D |
3.为迎接2019年全国青运会,我市加紧城市建设的步伐,某城区对一条全长1200m的公路进行绿化带改造,计划每天完成绿化带改造任务xm,当x满足的方程为$\frac{2}{3}$×$\frac{12000}{x}$=$\frac{12000}{x+300}$时,下列对这一方程所反映的数量关系描述正确的是( )
| A. | 实际每天比计划多完成改造任务300m,实际所用天数是计划的$\frac{2}{3}$ | |
| B. | 实际每天比计划少完成改造任务300m,计划所用天数是实际的$\frac{2}{3}$ | |
| C. | 实际每天比计划多完成改造任务300m,计划所用天数是实际的$\frac{2}{3}$ | |
| D. | 实际每天比计划少完成改造任务300m,实际所用天数是计划的$\frac{2}{3}$ |
13.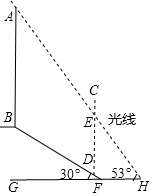 如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线AC与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为( )
如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线AC与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为( )
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,$\sqrt{3}$≈1.73)
 如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线AC与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为( )
如图,在坡角为30°的山坡FB上有一座信号塔AB,其右侧有一堵防护墙CD,测得BD的长度是30米,当光线AC与水平地面的夹角为53°时,测得信号塔落在防护墙上的影子DE的长为19米,则信号塔AB的高度约为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,$\sqrt{3}$≈1.73)
| A. | 35.5米 | B. | 37.6米 | C. | 38.6米 | D. | 40.3米 |
20.下列图形是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图所示,圆的半径为2,圆的两条弦AB,CD互相垂直,垂足为E.若圆心O到弦AB的距离OF=1,EF=1.则图中阴影部分的面积等于7.23(π取3.14)
如图所示,圆的半径为2,圆的两条弦AB,CD互相垂直,垂足为E.若圆心O到弦AB的距离OF=1,EF=1.则图中阴影部分的面积等于7.23(π取3.14)
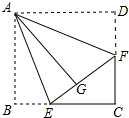 如图正方形ABCD的边长为4,点E、F分别在BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1.
如图正方形ABCD的边长为4,点E、F分别在BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知BE=1.