题目内容
 如图,在菱形ABCD中,E、F分别在BC、CD上,且△AEF是等边三角形,AE=AB,则∠BAD的度数是
如图,在菱形ABCD中,E、F分别在BC、CD上,且△AEF是等边三角形,AE=AB,则∠BAD的度数是考点:菱形的性质,等边三角形的性质
专题:
分析:利用菱形以及等边三角形的性质用x表示出∠B和∠BAD,进而得出答案.
解答: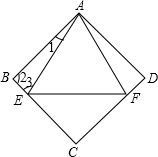 解:如图所示:∵在菱形ABCD中,E、F分别在BC、CD上,且△AEF是等边三角形,AE=AB,
解:如图所示:∵在菱形ABCD中,E、F分别在BC、CD上,且△AEF是等边三角形,AE=AB,
∴AB=AD=AE=AF,∠2=∠3=∠D=∠AFD,∠EAF=∠AEF=∠AFE=60°,
设∠2=x,则∠2=∠3=∠D=∠AFD=x,
故∠1=180°-2x,则∠DAF=180°-2x,
∵AD∥BC,
∴∠2+∠1+∠EAF+∠DAF=180°,
∴x+2(180°-2x)+60°=180°,
解得:x=80°,
则∠BAD=100°.
故答案为:100°.
 解:如图所示:∵在菱形ABCD中,E、F分别在BC、CD上,且△AEF是等边三角形,AE=AB,
解:如图所示:∵在菱形ABCD中,E、F分别在BC、CD上,且△AEF是等边三角形,AE=AB,∴AB=AD=AE=AF,∠2=∠3=∠D=∠AFD,∠EAF=∠AEF=∠AFE=60°,
设∠2=x,则∠2=∠3=∠D=∠AFD=x,
故∠1=180°-2x,则∠DAF=180°-2x,
∵AD∥BC,
∴∠2+∠1+∠EAF+∠DAF=180°,
∴x+2(180°-2x)+60°=180°,
解得:x=80°,
则∠BAD=100°.
故答案为:100°.
点评:此题主要考查菱形的性质及等边三角形的判定的理解及运用,难度一般.

练习册系列答案
相关题目
计算-1
×(
+1
-
) 的结果是( )
| 1 |
| 7 |
| 7 |
| 8 |
| 3 |
| 4 |
| 7 |
| 12 |
A、-
| ||
| B、0 | ||
| C、1 | ||
D、
|
Rt△ABC两直角边的长分别为6cm和8cm,则连接这两条直角边中点的线段长为( )
| A、10cm | B、3cm |
| C、4cm | D、5cm |
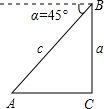 如图所示,飞行员在飞机B上用雷达测得飞机与目标城市A的距离c为4.5×102m,且测得对这个目标的俯角α=45°,设地面是平的,求飞机此时的高度a.
如图所示,飞行员在飞机B上用雷达测得飞机与目标城市A的距离c为4.5×102m,且测得对这个目标的俯角α=45°,设地面是平的,求飞机此时的高度a. 如图,函数y=-(x-h)2+k的图象,则其解析式为
如图,函数y=-(x-h)2+k的图象,则其解析式为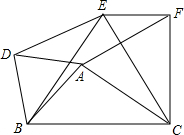 如图,以△ABC的三边为边在BC同一侧分别作三个等边三角形△ABD、△BCE、△ACF.
如图,以△ABC的三边为边在BC同一侧分别作三个等边三角形△ABD、△BCE、△ACF. 如图,边长为2正方形ABCD中,BD为对角线,AE∥BD,且DE=DB,DE与AB交于F点,则EF=
如图,边长为2正方形ABCD中,BD为对角线,AE∥BD,且DE=DB,DE与AB交于F点,则EF=