题目内容
 如图,边长为2正方形ABCD中,BD为对角线,AE∥BD,且DE=DB,DE与AB交于F点,则EF=
如图,边长为2正方形ABCD中,BD为对角线,AE∥BD,且DE=DB,DE与AB交于F点,则EF=考点:正方形的性质,含30度角的直角三角形,勾股定理,相似三角形的判定与性质
专题:
分析:根据正方形的性质求出∠DAE=135°,DE=2
,借助余弦定理求出AE的长度;利用相似三角形的性质求出EF的长度.
| 2 |
解答:解:∵四边形ABCD是正方形,
∴∠C=∠DAB=90°,∠ABD=45°;
又∵AE∥BD,
∴∠BAE=∠ABD=45°,
∴∠DAE=135°;
由勾股定理得:BD=
=
=2
;
故DE=BD=2
;
设AE=x,由余弦定理得:
(2
)2=22+x2-2×2xcos135°,
整理得:x2+2
x-4=0,
解得x=
-
或-
-
(不合题意,舍去);
设EF=y,则AF=2
-x\;
∵AE∥DB,
∴△AEF∽△BDF,
∴
=
,即
=
,
解得y=4
-2
.
故所求的答案为4
-2
.
∴∠C=∠DAB=90°,∠ABD=45°;
又∵AE∥BD,
∴∠BAE=∠ABD=45°,
∴∠DAE=135°;
由勾股定理得:BD=
| 22+22 |
| 8 |
| 2 |
故DE=BD=2
| 2 |
设AE=x,由余弦定理得:
(2
| 2 |
整理得:x2+2
| 2 |
解得x=
| 6 |
| 2 |
| 6 |
| 2 |
设EF=y,则AF=2
| 2 |
∵AE∥DB,
∴△AEF∽△BDF,
∴
| AE |
| BD |
| EF |
| DF |
| ||||
2
|
| y | ||
2
|
解得y=4
| 2 |
| 6 |
故所求的答案为4
| 2 |
| 6 |
点评:考查了正方形的性质、相似三角形的性质及其应用问题;解题的关键是首先借助余弦定理求出AE的长度,然后利用相似三角形的性质求出EF的长度;对综合运用能力提出了较高的要求.

练习册系列答案
相关题目
 如图,在菱形ABCD中,E、F分别在BC、CD上,且△AEF是等边三角形,AE=AB,则∠BAD的度数是
如图,在菱形ABCD中,E、F分别在BC、CD上,且△AEF是等边三角形,AE=AB,则∠BAD的度数是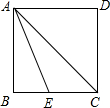 如图,已知:正方形ABCD中,∠BAC的平分线交BC于E,求证:AB+BE=AC.
如图,已知:正方形ABCD中,∠BAC的平分线交BC于E,求证:AB+BE=AC. 化简并求值:
化简并求值: 如图,在△ABC中,点P是△ABC的外角∠DBC、∠BCE的平分线的交点,若∠BPC=70°,则∠BAC=
如图,在△ABC中,点P是△ABC的外角∠DBC、∠BCE的平分线的交点,若∠BPC=70°,则∠BAC=