题目内容
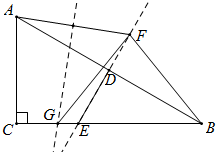 已知如图,在Rt△ABC中,∠C=90°,∠B=30°,D为AB的中点,E为BC上一点,且DE⊥AB,垂足为D.点F在ED的延长线上,连接BF、AF,作AF的垂直平分线交EC于点G,连接FG,请探究BF与FG之间的数量关系,并证明你的结论.
已知如图,在Rt△ABC中,∠C=90°,∠B=30°,D为AB的中点,E为BC上一点,且DE⊥AB,垂足为D.点F在ED的延长线上,连接BF、AF,作AF的垂直平分线交EC于点G,连接FG,请探究BF与FG之间的数量关系,并证明你的结论.考点:勾股定理
专题:
分析:连接AG,作FJ⊥AC,垂足为J,作FH⊥BC,垂足为H,得四边形CHFJ为矩形,设AC=1,在Rt△ABC中,∠ABC=30°,∴AB=2,由勾股定理得:BC=
,∵DE是AB的中垂线,∴AF=BF,∵GM是AF的中垂线,∴AG=FG,设BH=x,GH=y,FH=z,在Rt△BFH中:BF2=FH2+BH2=x2+z2;在Rt△FHG中:FG2=FH2+HG2=z2+y2;在Rt△AJF中:AF2=AJ2+JF2=(
-x)2+(1-z)2;在Rt△ACG中:AG2=AC2+CG2=1+(
-x-y)2,由AF=BF,AG=GF,得到AF2=BF2,AG2=GF2,然后将x,y,z代换即可.
| 3 |
| 3 |
| 3 |
解答:答:BF=FG.
证明:连接AG,作FJ⊥AC,垂足为J,作FH⊥BC,垂足为H,得四边形CHFJ为矩形,
∴CH=JF,JC=FH.
设AC=1,在Rt△ABC中,∠ABC=30°,
∴AB=2,
由勾股定理得:BC=
,
∵DE是AB的中垂线,
∴AF=BF,
∵GM是AF的中垂线,
∴AG=FG,
设BH=x,GH=y,FH=z,
在Rt△BFH中:BF2=FH2+BH2=x2+z2;
在Rt△FHG中:FG2=FH2+HG2=z2+y2;
在Rt△AJF中:AF2=AJ2+JF2=(
-x)2+(1-z)2;
在Rt△ACG中:AG2=AC2+CG2=1+(
-x-y)2,
∵AF=BF,AG=GF,
∴AF2=BF2,AG2=GF2,
即:x2+z2=(
-x)2+(1-z)2 ①,
z2+y2=1+(
-x-y)2 ②,
化简①得:z=2-
x ③,
将③代入②得:x2-
x+
y-xy=0,
即x(x-y)-
(x-y)=0,
(x-y)(x-
)=0,
∴x=y,
∴BH=GH,
∵FH⊥BG,
∴FH是BG的中垂线,
∴BF=FG
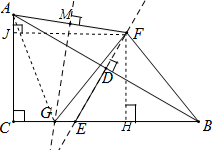
证明:连接AG,作FJ⊥AC,垂足为J,作FH⊥BC,垂足为H,得四边形CHFJ为矩形,
∴CH=JF,JC=FH.
设AC=1,在Rt△ABC中,∠ABC=30°,
∴AB=2,
由勾股定理得:BC=
| 3 |
∵DE是AB的中垂线,
∴AF=BF,
∵GM是AF的中垂线,
∴AG=FG,
设BH=x,GH=y,FH=z,
在Rt△BFH中:BF2=FH2+BH2=x2+z2;
在Rt△FHG中:FG2=FH2+HG2=z2+y2;
在Rt△AJF中:AF2=AJ2+JF2=(
| 3 |
在Rt△ACG中:AG2=AC2+CG2=1+(
| 3 |
∵AF=BF,AG=GF,
∴AF2=BF2,AG2=GF2,
即:x2+z2=(
| 3 |
z2+y2=1+(
| 3 |
化简①得:z=2-
| 3 |
将③代入②得:x2-
| 3 |
| 3 |
即x(x-y)-
| 3 |
(x-y)(x-
| 3 |
∴x=y,
∴BH=GH,
∵FH⊥BG,
∴FH是BG的中垂线,
∴BF=FG

点评:此题考查勾股定理的应用,解题的关键是构造直角三角形,利用勾股定理列关系式.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
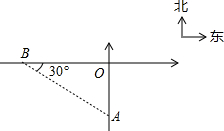 如图,钓鱼岛A在我某雷达站B东偏南30°方向400公里处,我歼10飞机在钓鱼岛A处巡逻时,被告知,某未通告飞行物从雷达站正东方飞来,0.2小时后即将达到我防空识别区边缘点O.已知∠AOB=90°,问我歼10飞机至少应以什么速度飞行才可以在其刚进入我识别区时予以识别?
如图,钓鱼岛A在我某雷达站B东偏南30°方向400公里处,我歼10飞机在钓鱼岛A处巡逻时,被告知,某未通告飞行物从雷达站正东方飞来,0.2小时后即将达到我防空识别区边缘点O.已知∠AOB=90°,问我歼10飞机至少应以什么速度飞行才可以在其刚进入我识别区时予以识别?