题目内容
要知道一组数据的离散程度,也可以求这组数据的“平均偏差”,平均偏差越大,数据的离散程度越大,越不稳定,反之,数据的离散程度越小.
求平均偏差的方法:已知数据x1,x2,…,xn,则平均偏差=
,运用平均偏差,比较下列两组数据的波动大小.
甲:0,1,2,3,4.
乙:0,2,4,6,8.
求平均偏差的方法:已知数据x1,x2,…,xn,则平均偏差=
|x1-
| ||||||
| n |
甲:0,1,2,3,4.
乙:0,2,4,6,8.
考点:方差
专题:新定义
分析:根据平均偏差的计算公式,先求出平均数,再代入公式计算,然后根据平均偏差的意义,数值较小的波动较小.
解答:解:∵
=
=2,
∴甲的平均偏差=
=1.2;
∵
=
=4,
∴乙的平均偏差=
=2.4;
∵1.2<2.4,
∴甲的波动较小.
. |
| x甲 |
| 0+1+2+3+4 |
| 5 |
∴甲的平均偏差=
| |0-2|+|1-2|+|2-2|+|3-2|+|4-2| |
| 5 |
∵
. |
| x乙 |
| 0+2+4+6+8 |
| 5 |
∴乙的平均偏差=
| |0-4|+|2-4|+|4-4|+|6-4|+|8-4| |
| 5 |
∵1.2<2.4,
∴甲的波动较小.
点评:本题考查学生的阅读理解能力、知识的迁移能力及平均偏差的意义.根据题意能够正确理解平均偏差的意义及计算公式是解题的关键.

练习册系列答案
相关题目
 如图所示,某水库大坝的横断面是梯形,坝顶AD宽2.5m,坝高4m,背水坡的坡度是1:1,迎水坡的坡度是1:1.5,求坝底宽BC.
如图所示,某水库大坝的横断面是梯形,坝顶AD宽2.5m,坝高4m,背水坡的坡度是1:1,迎水坡的坡度是1:1.5,求坝底宽BC.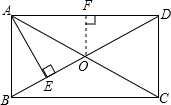 如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BO于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,求BD的长.
如图,在矩形ABCD中,对角线AC、BD交于点O,自点A作AE⊥BO于点E,且BE:ED=1:3,过点O作OF⊥AD于点F,若OF=3cm,求BD的长. 如图,点P为圆上的一个动点,弦AB=
如图,点P为圆上的一个动点,弦AB=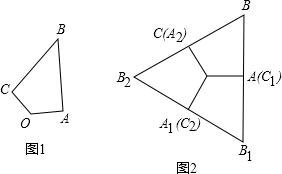 如图1,四边形ABCO中,∠A=∠C=90°,OA=1,AB=
如图1,四边形ABCO中,∠A=∠C=90°,OA=1,AB=