题目内容
4.用换元法解方程$\frac{{{x^2}-1}}{x}-\frac{2x}{{{x^2}-1}}=3$时,如果设$\frac{{{x^2}-1}}{x}=y$,那么原方程可化为关于y的整式方程,它可以是y2-3y-2=0.分析 将分式方程中的$\frac{{x}^{2}-1}{x}$换为y,$\frac{2x}{{x}^{2}-1}$换为$\frac{2}{y}$,去分母即可得到结果.
解答 解:根据题意得:y-$\frac{2}{y}$=3,
去分母得:y2-3y-2=0.
故答案为:y2-3y-2=0.
点评 此题考查了换元法解分式方程,用换元法解一些复杂的分式方程是比较简单的一种方法,根据方程特点设出相应未知数,解方程能够使问题简单化,注意求出方程解后要验根.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
15.下列命题是真命题的是( )
| A. | 两条不相交的直线就是平行线 | |
| B. | 过任意一点可以作已知直线的一条平行线 | |
| C. | 过直线外任意一点作已知直线的垂线,可以作无数条 | |
| D. | 直线外一点与直线上各点所连接的所有线段中,垂线段最短 |
12.已知直角三角形两边的长分别为5、12,则第三边的长为( )
| A. | 13 | B. | 60 | C. | 17 | D. | 13或$\sqrt{119}$ |
19.学校需要测量升旗杆的高度.同学们发现系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.经测量,绳子多出的部分长度为2m,将绳子沿地面拉直,绳子底端距离旗杆底端6m,求旗杆的高度.
9.下列方程中,其解为-2的是( )
| A. | $\frac{x+5}{3}-1=0$ | B. | 3(x+1)-3=0 | C. | 3x-4=2 | D. | 2x=-1 |
16.小于5的正整数有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.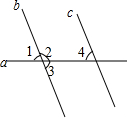 如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )
如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )
 如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )
如图,已知直线b,c被直线a所截,∠1=65°,若要判断b∥c,则下列所给条件正确的是( )| A. | ∠2=115° | B. | ∠3=65° | C. | ∠4=65° | D. | ∠4=115° |
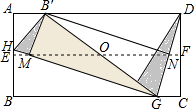 数学活动课上,老师组织各学习小组同学动手操作,大胆猜想并加以验证.
数学活动课上,老师组织各学习小组同学动手操作,大胆猜想并加以验证.