题目内容
12.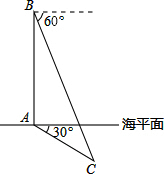 在一次军事演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方
在一次军事演习中,我军舰A测得潜艇C的俯角为30°,位于军舰A正上方 1000m的反潜直升机B测得潜艇C的俯角为60°,求潜艇C离开海平面的下潜深度.
分析 过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,分别在Rt△ACD中表示出CD和在Rt△BCD中表示出BD,从而利用二者之间的关系列出方程求解.
解答 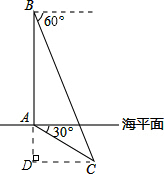 解:过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,
解:过点C作CD⊥AB,交BA的延长线于点D,则AD即为潜艇C的下潜深度,
根据题意得:∠ACD=30°,∠BCD=60°,
设AD=x,则BD=BA+AD=1000+x,
在Rt△ACD中,CD=$\frac{AD}{tan∠ACD}$=$\frac{x}{tan30°}$=$\sqrt{3}$x,
在Rt△BCD中,BD=CD•tan60°,
∴1000+x=$\sqrt{3}$x•tan60°
解得:x=500,
∴潜艇C离开海平面的下潜深度为500米.
点评 本题考查了解直角三角形的应用,解题的关键是从题目中抽象出直角三角形并选择合适的边角关系求解.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
2.已知一个等腰三角形有一个角为80°,则顶角是( )
| A. | 20° | B. | 80° | C. | 20°或80° | D. | 不能确定 |
17.下列运算正确的是( )
| A. | a2+a3=a5 | B. | a6÷a2=a3 | C. | (-a2)3=a6 | D. | -2a•a2=-2a3 |
1.化简a2•a的结果是( )
| A. | a2 | B. | 2a2 | C. | a3 | D. | a |
2.在$-\sqrt{2}$,$-\frac{1}{2}$,0,-0.2四个数中,最大的数是( )
| A. | 0 | B. | $-\frac{1}{2}$ | C. | $-\sqrt{2}$ | D. | -0.2 |


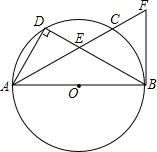 如图,AB是⊙O的直径,点C在⊙O上,点D是$\widehat{AC}$的中点,连接AD,BD.射线AC与BD相交于点E,与⊙O过点B的切线相交于点F,DE=4,BE=8.
如图,AB是⊙O的直径,点C在⊙O上,点D是$\widehat{AC}$的中点,连接AD,BD.射线AC与BD相交于点E,与⊙O过点B的切线相交于点F,DE=4,BE=8.