题目内容
14.把几个数用大括号括起来,相邻两个数之间用逗号隔开,如:{1,2},{1,4,7},…,我们称之为集合,其中的每一个数称为该集合的元素,如果一个所有元素均为有理数的集合满足:当有理数x是集合的一个元素时,2016-x也必是这个集合的元素,这样的集合我们又称为黄金集合.例如{0,2016}就是一个黄金集合,(1)集合{2016}不是黄金集合,集合{-1,2017}是黄金集合;(两空均填“是”或“不是”)
(2)若一个黄金集合中最大的一个元素为4016,则该集合是否存在最小的元素?如果存在,请直接写出答案,否则说明理由;
(3)若一个黄金集合所有元素之和为整数M,且24190<M<24200,则该集合共有几个元素?说明你的理由.
分析 (1)根据有理数a是集合的元素时,2016-a也必是这个集合的元素,这样的集合我们称为黄金集合,从而可以解答本题;
(2)根据2016-a,如果a的值越大,则2016-a的值越小,从而可以解答本题;
(3)根据题意可知黄金集合都是成对出现的,并且这对对应元素的和为2016,然后通过估算即可解答本题.
解答 解:(1)根据题意可得,2016-2016=0,而集合{2016}中没有元素0,故{2016}不是黄金集合;
∵2016-2017=-1,
∴集合{-1,2017}是黄金集合.
故答案为:不是,是.
(2)一个黄金集合中最大的一个元素为4016,则该集合存在最小的元素,该集合最小的元素是-2000.
∵2016-a中a的值越大,则2016-a的值越小,
∴一个黄金集合中最大的一个元素为4016,则最小的元素为:2016-4016=-2000.
(3)该集合共有24个元素.
理由:∵在黄金集合中,如果一个元素为a,则另一个元素为2016-a,
∴黄金集合中的元素一定是偶数个.
∵黄金集合中的每一对对应元素的和为:a+2016-a=2016,2016×12=24192,2016×13=26208,
又∵一个黄金集合所有元素之和为整数M,且24190<M<24200,
∴这个黄金集合中的元素个数为:12×2=24(个).
点评 本题考查了有理数以及探究性问题,关键是明确什么是黄金集合,集合中的各个数都是元素,明确黄金集合中的元素个数都是偶数个,在此还要应用到估算的知识.

练习册系列答案
相关题目
5.216表示( )
| A. | 2乘以16 | B. | 2个16相乘 | C. | 16个2相加 | D. | 16个2相乘 |
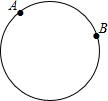 如图,已知一周长为30cm的圆形轨道上有相距10cm的A、B两点(备注:圆形轨道上两点间的距离是指圆上这两点间的较短部分展直后的线段长).动点P从A点出发,以acm/s的速度,在轨道上逆时针方向运动,与此同时,动点Q从B点出发,以3cm/s的速度,按同样的方向运动,设运动时间为t(s),当t=5时,动点P、Q第一次相遇.
如图,已知一周长为30cm的圆形轨道上有相距10cm的A、B两点(备注:圆形轨道上两点间的距离是指圆上这两点间的较短部分展直后的线段长).动点P从A点出发,以acm/s的速度,在轨道上逆时针方向运动,与此同时,动点Q从B点出发,以3cm/s的速度,按同样的方向运动,设运动时间为t(s),当t=5时,动点P、Q第一次相遇. 如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,OD⊥BC于E.
如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,OD⊥BC于E. 如图,点A、B、C在⊙O上,∠C=115°,则∠AOB=130°.
如图,点A、B、C在⊙O上,∠C=115°,则∠AOB=130°.