题目内容
15．
如图，在△ABC中，AB=AC，AD平分∠BAC，DE∥AC交AB于点E，则S△EBD：S△ABC=1：4．
分析 先根据等腰三角形的性质得出D点时BC的中点，故可得出△BDE∽△BCA，再由相似三角形的性质即可得出结论．
解答 解：∵在△ABC中，AB=AC，AD平分∠BAC，
∴点D是BC的中点．
∵DE∥AC，
∴△BDE∽△BCA，其相似比为1：2，
∴S△EBD：S△ABC=1：4．
故答案为：1：4．
点评 本题考查的是相似三角形的判定与性质，熟知相似三角形面积的比等于相似比的平方是解答此题的关键．
练习册系列答案
优学名师名题系列答案
相关题目
7．下列图形一定是轴对称图形的是（ ）
| A． | 直角三角形 | B． | 平行四边形 | C． | 直角梯形 | D． | 正方形 |
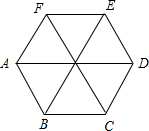如图是由边长为4的六个等边三角形组成的六边形，建立适当的直角坐标系，写出顶点A、B、F的坐标．
如图，在△ABC中，∠B=42°，∠C=78°，AD平分∠BAC．
5．化简$\frac{x}{x-1}-\frac{1}{1-x}$的结果为（ ）
| A． | -1 | B． | 1 | C． | $\frac{x+1}{x-1}$ | D． | $\frac{x+1}{1-x}$ |