题目内容
9. 一副三角板,按如图所示摆放,已知AB=2,则CD=$\sqrt{6}$.
一副三角板,按如图所示摆放,已知AB=2,则CD=$\sqrt{6}$.
分析 先在Rt△ABC中利用∠ACB的正切计算出BC,然后在Rt△BCD中利用∠BCD的余弦计算CD的长.
解答 解:在Rt△ABC中,∵tan∠ACB=$\frac{AB}{BC}$,
∴BC=$\frac{2}{tan30°}$=$\frac{2}{\frac{\sqrt{3}}{3}}$2$\sqrt{3}$,
在Rt△BCD中,∵cos∠BCD=$\frac{CD}{BC}$,
∴CD=2$\sqrt{3}$•cos45°=2$\sqrt{3}$×$\frac{\sqrt{2}}{2}$=$\sqrt{6}$.
故答案为$\sqrt{6}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.灵活由于勾股定理、互余关系和三角函数关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.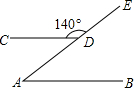 如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )
如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )
 如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )
如图,点A、D在射线AE上,直线AB∥CD,∠CDE=140°,那么∠A的度数为( )| A. | 140° | B. | 60° | C. | 50° | D. | 40° |
6.某新办高新产业2011年的两笔贷款记录如下表:
(1)求两笔贷款的数额各是多少?
(2)已知这两笔贷款的20%用于6月1日前的科研开发,另一部分从6月至11月投入生产新研发出的A、B种新专利产品,新产品的成本与出厂价如上表.到12月1日卖出所有产品,所获利润偿还两笔贷款后,还余200万元.求:两种产品的产量各是多少件?
| 贷款日期 | 月利率% | 还款日期 | 贷款金额(万元) | 还款金额(万元) |
| 4月1日 | 1.5 | 12月1日 | ||
| 6月1日 | 1 | 12月1日 | ||
| 合计 | 300 | 330 |
| A(元) | B(元) | |
| 单件成本 | 3000 | 2000 |
| 单件出厂价 | 6500 | 6000 |
 如图,同学们上体育课时,老师测量学生的跳远成绩,其测量的主要依据是垂线段最短.
如图,同学们上体育课时,老师测量学生的跳远成绩,其测量的主要依据是垂线段最短.