题目内容
17．已知m=$\frac{3n+25}{2n-5}$是正整数，那么n可以取4种不同的正整数．分析 将m化为1+$\frac{n+30}{2n-5}$，当n+30=2n-5时，n=35；当n+30＞2n-5时，n＜35；当n+30＜2n-5时，n＞35（不可能是正整数）；计算可得n的整整数值．
解答 解：当n=3时，m=$\frac{3n+25}{2n-5}$=34；
当n=5时，m=$\frac{3n+25}{2n-5}$=8；
当n=9时，m=$\frac{3n+25}{2n-5}$=4；
当n=35时，m=$\frac{3n+25}{2n-5}$=2；
当n=3，5，9，35时，m=$\frac{3n+25}{2n-5}$时正整数；
故答案为4．
点评 本题考查了分式的值，确定m，n的值是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
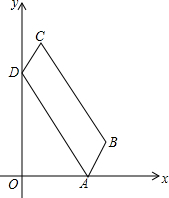如图，在?ABCD中，∠BAD=60°，点A在x轴的正半轴上，点D在y轴的正半轴上，tan∠OAD=$\sqrt{3}$，AD和DC的长分别是方程x2-8x+12=0的两个根（AD＞DC）．
一副三角板，按如图所示摆放，已知AB=2，则CD=$\sqrt{6}$．