题目内容
1. 如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为-6.
如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为-6.
分析 连接AC,交y轴于点D,由四边形ABCO为菱形,得到对角线垂直且互相平分,得到三角形CDO面积为菱形面积的四分之一,根据菱形面积求出三角形CDO面积,利用反比例函数k的几何意义确定出k的值即可.
解答  解:连接AC,交y轴于点D,
解:连接AC,交y轴于点D,
∵四边形ABCO为菱形,
∴AC⊥OB,且CD=AD,BD=OD,
∵菱形OABC的面积为12,
∴△CDO的面积为3,
∴|k|=6,
∵反比例函数图象位于第二象限,
∴k<0,
则k=-6.
故答案为:-6.
点评 此题考查了反比例函数系数k的几何意义,以及菱形的性质,熟练掌握反比例函数k的几何意义是解本题的关键.

练习册系列答案
相关题目
9.不等式组$\left\{\begin{array}{l}{3x<2x+4}\\{\frac{3-x}{3}≥2}\end{array}\right.$的解集,在数轴上表示正确的是( )
| A. |  | B. |  | ||
| C. |  | D. | 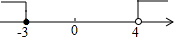 |
10.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )
| A. | 7 | B. | 7或8 | C. | 8或9 | D. | 7或8或9 |
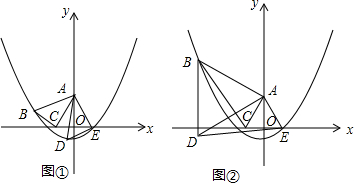
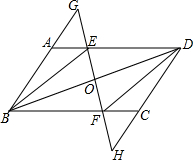 已知:如图,在?ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.
已知:如图,在?ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O. 如图,是我们数学课本上采用的科学计算器面板,利用该型号计算器计算$\sqrt{2}$cos55°,按键顺序正确的是( )
如图,是我们数学课本上采用的科学计算器面板,利用该型号计算器计算$\sqrt{2}$cos55°,按键顺序正确的是( )