题目内容
6.若二次函数y=2x2-4x-1的图象与x轴交于A(x1,0)、B(x2,0)两点,则$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值为-4.分析 设y=0,则对应一元二次方程的解分别是点A和点B的横坐标,利用根与系数的关系即可求出$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的值.
解答 解:
设y=0,则2x2-4x-1=0,
∴一元二次方程的解分别是点A和点B的横坐标,即x1,x2,
∴x1+x2=-$\frac{-4}{2}$=2,x1,•x2=-$\frac{1}{2}$,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=-4,
故答案为:-4.
点评 本题考查了二次函数与一元二次方程的关系,掌握二次函数与x轴的交点的横坐标就是对应的一元二次方程的根是解题关键.

练习册系列答案
相关题目
14.下列实数中,有理数是( )
| A. | $\sqrt{8}$ | B. | $\root{3}{4}$ | C. | $\frac{π}{2}$ | D. | 0.101001001 |
18.在实数-$\frac{1}{3}$,-2,0,$\sqrt{3}$中,最小的实数是( )
| A. | -2 | B. | 0 | C. | -$\frac{1}{3}$ | D. | $\sqrt{3}$ |
 如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(5,0),菱形OABC的顶点B,C都在第一象限,tan∠AOC=$\frac{4}{3}$,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG.
如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(5,0),菱形OABC的顶点B,C都在第一象限,tan∠AOC=$\frac{4}{3}$,将菱形绕点A按顺时针方向旋转角α(0°<∠α<∠AOC)得到菱形FADE(点O的对应点为点F),EF与OC交于点G,连结AG.
 如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为-6.
如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为-6. 如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP的长不可能是( )
如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP的长不可能是( )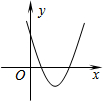 二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数$y=-\frac{a}{x}$与一次函数y=bx-c在同一坐标系内的图象大致是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数$y=-\frac{a}{x}$与一次函数y=bx-c在同一坐标系内的图象大致是( )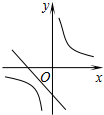
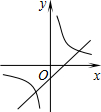
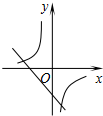
 如图,⊙O1和⊙O2相交于点A和B,直线CD经过点A,且交⊙O1于点C,交⊙O2于点D,CD⊥AB,求证:CD=2O1O2.
如图,⊙O1和⊙O2相交于点A和B,直线CD经过点A,且交⊙O1于点C,交⊙O2于点D,CD⊥AB,求证:CD=2O1O2.