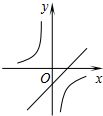题目内容
10.一个多边形切去一个角后,形成的另一个多边形的内角和为1080°,那么原多边形的边数为( )| A. | 7 | B. | 7或8 | C. | 8或9 | D. | 7或8或9 |
分析 首先求得内角和为1080°的多边形的边数,即可确定原多边形的边数.
解答 解:设内角和为1080°的多边形的边数是n,则(n-2)•180°=1080°,
解得:n=8.
则原多边形的边数为7或8或9.
故选:D.
点评 本题考查了多边形的内角和定理,一个多边形截去一个角后它的边数可能增加1,可能减少1,或不变.

练习册系列答案
 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
20.计算(-2)0+9÷(-3)的结果是( )
| A. | -1 | B. | -2 | C. | -3 | D. | -4 |
18.在实数-$\frac{1}{3}$,-2,0,$\sqrt{3}$中,最小的实数是( )
| A. | -2 | B. | 0 | C. | -$\frac{1}{3}$ | D. | $\sqrt{3}$ |
2.据市统计局调查数据显示,我市目前常住人口约为4470000人,数据“4470000”用科学记数法可表示为( )
| A. | 4.47×106 | B. | 4.47×107 | C. | 0.447×107 | D. | 447×104 |
8.化简2$\sqrt{8}$-$\sqrt{2}$-3$\sqrt{50}$-$\sqrt{12}$+$\sqrt{18}$的结果为( )
| A. | -$\sqrt{11}$ | B. | -9$\sqrt{2}$-2$\sqrt{3}$ | C. | -7$\sqrt{2}$ | D. | 2$\sqrt{3}$-9$\sqrt{2}$ |
 如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为-6.
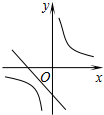
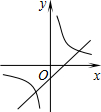
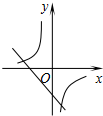
如图,在平面直角坐标系中,菱形OABC的面积为12,点B在y轴上,点C在反比例函数y=$\frac{k}{x}$的图象上,则k的值为-6.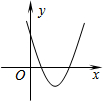 二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数$y=-\frac{a}{x}$与一次函数y=bx-c在同一坐标系内的图象大致是( )
二次函数y=ax2+bx+c(a≠0)的图象如图,则反比例函数$y=-\frac{a}{x}$与一次函数y=bx-c在同一坐标系内的图象大致是( )