题目内容
4.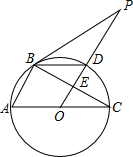 如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.
如图,△ABC内接于⊙O,AC为⊙O的直径,PB是⊙O的切线,B为切点,OP⊥BC,垂足为E,交⊙O于D,连接BD.(1)求证:BD平分∠PBC;
(2)若⊙O的半径为1,PD=3DE,求OE及AB的长.
分析 (1)由∠PBD+∠OBD=90°,∠DBE+∠BDO=90°利用等角的余角相等即可解决问题.
(2)利用面积法首先证明$\frac{BE}{PB}$=$\frac{ED}{PD}$=$\frac{1}{3}$,再证明△BEO∽△PEB,得$\frac{BO}{PB}$=$\frac{OE}{BE}$,即$\frac{OE}{BO}$=$\frac{BE}{PB}$=$\frac{1}{3}$,由此即可解决问题.
解答 (1)证明:连接OB.
∵PB是⊙O切线,
∴OB⊥PB,
∴∠PBO=90°,
∴∠PBD+∠OBD=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∵OP⊥BC,
∴∠BED=90°,
∴∠DBE+∠BDE=90°,
∴∠PBD=∠EBD,
∴BD平分∠PBC.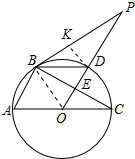
(2)解:作DK⊥PB于K,
∵$\frac{{S}_{△BDE}}{{S}_{△BDP}}$=$\frac{\frac{1}{2}BE•DE}{\frac{1}{2}PB•DK}$=$\frac{DE}{DP}$,
∵BD平分∠PBE,DE⊥BE,DK⊥PB,
∴DK=DE,
∴$\frac{BE}{PB}$=$\frac{ED}{PD}$=$\frac{1}{3}$(也可以利用sinP=$\frac{DK}{PD}$=$\frac{DE}{DP}$=$\frac{1}{3}$,推出$\frac{BE}{PB}$=$\frac{1}{3}$),
∵∠OBE+∠PBE=90°,∠PBE+∠P=90°,
∴∠OBE=∠P,∵∠OEB=∠BEP=90°,
∴△BEO∽△PEB,
∴$\frac{BO}{PB}$=$\frac{OE}{BE}$,
∴$\frac{OE}{BO}$=$\frac{BE}{PB}$=$\frac{1}{3}$,
∵BO=1,
∴OE=$\frac{1}{3}$,
∵OE⊥BC,
∴BE=EC,∵AO=OC,
∴AB=2OE=$\frac{2}{3}$.
点评 本题考查切线的性质、相似三角形的判定和性质、三角形中位线定理等知识,解题的关键是添加辅助线,学会利用面积法解决问题,属于中考常考题型.

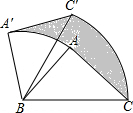 如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )
如图,在△ABC中,∠A=90°,AB=AC=3,现将△ABC绕B逆时针旋转一定角度,点C′恰好落在边BC上的高所在的直线上,则阴影部分的面积为( )| A. | π | B. | $\frac{3π}{2}$ | C. | $\frac{5π}{2}$ | D. | 3π |
| A. | x1=-3,x2=-1 | B. | x1=1,x2=3 | C. | x1=-1,x2=3 | D. | x1=-3,x2=1 |
| A. | -5 | B. | -8 | C. | -2 | D. | 5 |
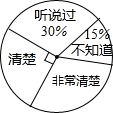 第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有2700人.
第十二届全国人大四次会议审议通过的《中华人民共和国慈善法》将于今年9月1日正式实施,为了了解居民对慈善法的知晓情况,某街道办从辖区居民中随机选取了部分居民进行调查,并将调查结果绘制成如图所示的扇形图.若该辖区约有居民9000人,则可以估计其中对慈善法“非常清楚”的居民约有2700人.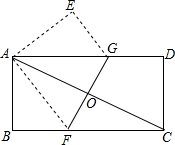 如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为6.
如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为6.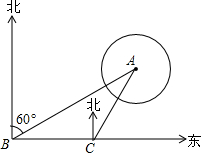 如图,某公园有一小亭A,它周围100米内是文物保持区,某勘探队员在公园由西向东行走,在B处测得小亭A在北偏东60°的方向上,行走200米后到达C处,此时测得小亭A在北偏东30°的方向上,若该公园打算沿BC的方向修一条笔直的小路,则此小路是否会通过文物保护区?请通过计算说明.
如图,某公园有一小亭A,它周围100米内是文物保持区,某勘探队员在公园由西向东行走,在B处测得小亭A在北偏东60°的方向上,行走200米后到达C处,此时测得小亭A在北偏东30°的方向上,若该公园打算沿BC的方向修一条笔直的小路,则此小路是否会通过文物保护区?请通过计算说明.