题目内容
2．圆内接正方形半径为2，则面积为（ ）| A． | 2 | B． | 4 | C． | 8 | D． | 16 |
分析 根据圆内接正方形的性质，得出∠BOC=90°，以及CB2即正方形的面积，求出即可．
解答 
解：过圆心O作OE⊥CB，
∵圆的半径为2，内接四边形是正方形，
∴∠BOC=90°，OB=OC，
∴∠OBC=∠OCB=45°，
∴22+22=CB2，
∴AB2=8，
即正方形的面积为：8．
故选：C．
点评 此题主要考查了圆内接正方形的性质，正方形与圆的有关计算，正确应用勾股定理是解题关键．
练习册系列答案
相关题目
10．下列命题是假命题的是（ ）
| A． | 互补的两个角不能都是锐角 | B． | 若a⊥b，a⊥c，则b⊥c | ||
| C． | 乘积是1的两个数互为倒数 | D． | 全等三角形的对应角相等 |
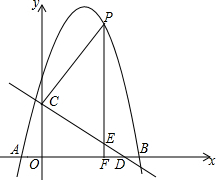如图，抛物线y=-x2+bx+c与x轴交于A（-1，0），B（5，0）两点，直线y=-$\frac{3}{4}$x+3与y轴交于点C，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m．
7．若8x3ym÷4xny2=2y2，则m，n的值为（ ）
| A． | m=1，n=3 | B． | m=4，n=3 | C． | m=4，n=2 | D． | m=3，n=4 |
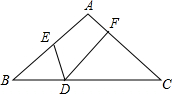如图：在△ABC中，AB=AC，点D、E、F分别在BC、AB、AC上，∠EDF=∠B．求证：BD•CD=BE•CF．
11．等腰三角形的一个角是70°，则它的底角是（ ）
| A． | 70° | B． | 70°或55° | C． | 80°和100° | D． | 110° |