题目内容
5.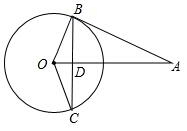 如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB=60°.
如图,AB与⊙O相切于点B,线段OA与弦BC垂直,垂足为D,AB=BC=2,则∠AOB=60°.
分析 由垂径定理易得BD=1,通过解直角三角形ABD得到∠A=30°,然后由切线的性质和直角三角形的两个锐角互余的性质可以求得∠AOB的度数.
解答 解:∵OA⊥BC,BC=2,
∴根据垂径定理得:BD=$\frac{1}{2}$BC=1.
在Rt△ABD中,sin∠A=$\frac{BD}{AB}$=$\frac{1}{2}$.
∴∠A=30°.
∵AB与⊙O相切于点B,
∴∠ABO=90°.
∴∠AOB=60°.
故答案是:60.
点评 本题主要考查的圆的切线性质,垂径定理和一些特殊三角函数值,有一定的综合性.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
15.如图所示的几何体,其俯视图是( )
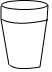

| A. | 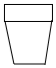 | B. | 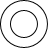 | C. |  | D. |  |
13.-5的倒数是( )
| A. | -5 | B. | 5 | C. | $\frac{1}{5}$ | D. | $-\frac{1}{5}$ |
17.计算$\frac{a}{a+1}+\frac{1}{a+1}$的结果为( )
| A. | 1 | B. | a | C. | a+1 | D. | $\frac{1}{a+1}$ |
14.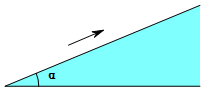 如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα=$\frac{12}{13}$,则小车上升的高度是( )
如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα=$\frac{12}{13}$,则小车上升的高度是( )
 如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα=$\frac{12}{13}$,则小车上升的高度是( )
如图,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cosα=$\frac{12}{13}$,则小车上升的高度是( )| A. | 5米 | B. | 6米 | C. | 6.5米 | D. | 12米 |
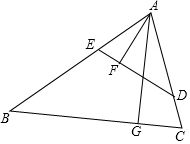 如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.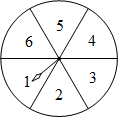 如图,转盘中6个扇形的面积相等,任意转动转盘1次,当转盘停止转动时,指针指向的数小于5的概率为$\frac{2}{3}$.
如图,转盘中6个扇形的面积相等,任意转动转盘1次,当转盘停止转动时,指针指向的数小于5的概率为$\frac{2}{3}$.
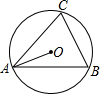 如图,△ABC内接于⊙O,若∠OAB=32°,则∠C=58°.
如图,△ABC内接于⊙O,若∠OAB=32°,则∠C=58°.