题目内容
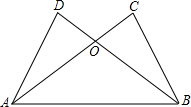如图，已知△ABC≌△BAD，AC与BD相交于点O，求证：OC=OD．考点：全等三角形的性质,等腰三角形的判定与性质
专题：证明题
分析：由△ABC≌△BAD，根据全等三角形的性质得出∠CAB=∠DBA，AC=BD，利用等角对等边得到OA=OB，那么AC-OA=BD-OB，即：OC=OD．
解答：
证明：∵△ABC≌△BAD，
∴∠CAB=∠DBA，AC=BD，
∴OA=OB，
∴AC-OA=BD-OB，
即：OC=OD．
∴∠CAB=∠DBA，AC=BD，
∴OA=OB，
∴AC-OA=BD-OB，
即：OC=OD．
点评：本题考查了全等三角形的性质：全等三角形的对应边相等，全等三角形的对应角相等．也考查了等腰三角形的判定及等式的性质．
练习册系列答案
相关题目
在长、宽都为4m，高为3m的房间的正中央的天花板上悬挂一只白炽灯泡A．为了集中光线，加上了灯罩，如图所示．已知灯罩深8cm，灯泡离地面2m，为了使光线恰好照在墙角，则灯罩的直径应为多少（DE、GF分别为地面与天花板的对角线．计算结果精确到0.01m）？
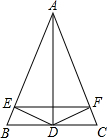如图，在△ABC中，AD平分∠BAC，DE⊥AB，DF⊥AC，E，F为垂足，则下列四个结论：（1）∠BAD=∠CAD；（2）ED=FD；（3）AD平分∠EDF；（4）AD，EF互相垂直平分．其中正确的有（ ）| A、1个 | B、2个 | C、3个 | D、4个 |
两根木棒的长分别是5cm和7cm，要选择第三根木棒，将他们首尾相接钉成一个三角形．则第三根木棒长的取值可以是（ ）
| A、2cm | B、4cm |
| C、12cm | D、13cm |
如图所示，∠DBC=2∠ABD，∠DCB=2∠ACD，若∠BDC=α+