题目内容
18. 如图,鹏鹏将长方形纸片ABCD剪成三角形纸片DEF,若∠DEF+∠EDF=90°,则∠EFB+∠DFC的度数为90°.
如图,鹏鹏将长方形纸片ABCD剪成三角形纸片DEF,若∠DEF+∠EDF=90°,则∠EFB+∠DFC的度数为90°.
分析 根据∠DEF+∠EDF=90°结合三角形内角和定理即可得出∠EFD=90°,再根据∠BFC为平角即可得出∠EFB+∠DFC=90°.
解答 解:∵∠DEF+∠EDF=90°,∠DEF+∠EDF+∠EFD=180°,
∴∠EFD=90°.
∵∠EFB+∠EFD+∠DFC=180°,
∴∠EFB+∠DFC=90°.
故答案为:90°.
点评 本题考查了三角形内角和定理,根据三角形内角和定理求出∠EFD=90°是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.25的平方根是( )
| A. | ±5 | B. | 5 | C. | ±$\sqrt{5}$ | D. | -5 |
6.在函数y=$\frac{-{a}^{2}-1}{x}$(a为常数)的图象上有三点A(-3,y1),B(-1,y2),C(3,y3),则函数值y1、y2、y3的大小关系是( )
| A. | y2<y3<y1 | B. | y3<y2<y1 | C. | y1<y2<y3 | D. | y3<y1<y2 |
13.已知△ABC≌△DEF,∠A=78°,∠B=35°,则∠F=( )
| A. | 78° | B. | 35° | C. | 77° | D. | 67° |
10.若(x-2)(x-1)=x2+mx+n,则m+n=( )
| A. | 1 | B. | -2 | C. | -1 | D. | 2 |
7.下列一组数是勾股数的是( )
| A. | 6,7,8 | B. | 5,12,13 | C. | 0.3,0.4,0.5 | D. | 10,15,18 |
8.下列命题中是假命题的是( )
| A. | 等腰三角形一边上的中线和高互相重合 | |
| B. | 等腰三角形的底角一定是锐角 | |
| C. | 有一条边相等的两个等边三角形全等 | |
| D. | 顶角相等,底边上的高也相等的两个等腰三角形全等 |
 将边长为1的正方形ABCD放在直角坐标系中,使C的坐标为($\frac{1}{2}$,$\frac{1}{2}$),请建立直角坐标系.并求其余各点的坐标.
将边长为1的正方形ABCD放在直角坐标系中,使C的坐标为($\frac{1}{2}$,$\frac{1}{2}$),请建立直角坐标系.并求其余各点的坐标.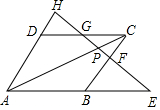 如图,过?ABCD的对角线AC上任一点P作一直线,分别交AB、BC、CD、DA所在直线于E、F、G、H.求证:PE•PF=PG•PH.
如图,过?ABCD的对角线AC上任一点P作一直线,分别交AB、BC、CD、DA所在直线于E、F、G、H.求证:PE•PF=PG•PH.