题目内容
4. 如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的负半轴上,点C在y轴的正半轴上,OA=5,OC=4,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的负半轴上,点C在y轴的正半轴上,OA=5,OC=4,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
分析 先根据勾股定理求出BE的长,进而可得出CE的长,求出E点坐标,在Rt△DCE中,由DE=OD及勾股定理可求出OD的长,进而得出D点坐标.
解答 解:依题意可知,折痕AD是四边形OAED的对称轴
∴DE=OD,AE=AO=5,AB=OC=4,
∴BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴CE=5-3=2,
∴E(-2,4).
在Rt△DCE中,DC2+CE2=DE2,
又∵DE=OD,
∴(4-OD)2+22=OD2,
∴OD=2.5,
∴D(0,2.5).
综上所述:D点坐标为(0,2.5),E点坐标为(-2,4).
点评 本题主要考查了翻折变换、勾股定理等知识点,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.

练习册系列答案
相关题目
9.下列图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

 如图,一张长方形桌子的桌面长100cm,宽60cm,一块长方形台布的面积是桌面面积是2$\frac{3}{4}$倍,并且铺在桌面上时,各边垂下的长度相等,求台布的长和宽.
如图,一张长方形桌子的桌面长100cm,宽60cm,一块长方形台布的面积是桌面面积是2$\frac{3}{4}$倍,并且铺在桌面上时,各边垂下的长度相等,求台布的长和宽.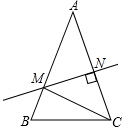 如图,在等腰△ABC中,∠A=40°,AC的垂直平分线MN交AB,AC于点M,N.则∠MCB=30°.
如图,在等腰△ABC中,∠A=40°,AC的垂直平分线MN交AB,AC于点M,N.则∠MCB=30°.