题目内容
14.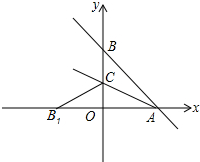 如图,直线y=-$\frac{4}{3}$x+4与x轴,y轴,分别交于A,B两点,点C是y轴上一点,沿直线AC折叠AB刚好落在x轴上AB1处.
如图,直线y=-$\frac{4}{3}$x+4与x轴,y轴,分别交于A,B两点,点C是y轴上一点,沿直线AC折叠AB刚好落在x轴上AB1处.(1)求A、B两点的坐标;
(2)求OC的长;
(3)在x轴上存在点P,使三角形PCA为等腰三角形,直接写出P的坐标.
分析 (1)对于直线解析式,分别令x与y为0,求出y与x的值,即可确定出A与B的坐标;
(2)在直角三角形AOB中,利用勾股定理求出AB的长,由折叠的性质得到∠BAC=∠B1AC,利用角平分线性质列出比例式,根据OB的长求出OC的长即可;
(3)在直角三角形AOC中,利用勾股定理求出AC的长,如图所示,分三种情况考虑:当AP=AC;当AP′=AC;当P″A=P″C,作AC的垂直平分线交OA于点P″,分别求出P的坐标即可.
解答  解:(1)对于直线y=-$\frac{4}{3}$x+4,
解:(1)对于直线y=-$\frac{4}{3}$x+4,
令x=0,得到y=4;令y=0,得到x=3,
则A(3,0),B(0,4);
(2)在Rt△ABC中,OA=3,OB=4,
根据勾股定理得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
由折叠的性质得:∠BAC=∠B1AC,
∴OC:CB=AO:AB=3:5,
则OC=4×$\frac{3}{8}$=1.5;
(3)在Rt△OAC中,OA=3,OC=1.5,
根据勾股定理得:AC=$\sqrt{{3}^{2}+1.{5}^{2}}$=$\frac{3\sqrt{5}}{2}$,
如图所示,要使△PAC为等腰三角形,分三种情况考虑:
当AP=AC时,P坐标为(3-$\frac{3\sqrt{5}}{2}$,0);
当AP′=AC时,P′坐标为(3+$\frac{3\sqrt{5}}{2}$,0);
当P″A=P″C时,作AC的垂直平分线交OA于点P″,
设OP″=x,根据勾股定理得:x2+1.52=(3-x)2,
解得:x=$\frac{9}{8}$,即P″($\frac{9}{8}$,0),
综上,点P的坐标为(3-$\frac{3\sqrt{5}}{2}$,0)或(3+$\frac{3\sqrt{5}}{2}$,0)或($\frac{9}{8}$,0)或(-3,0).
点评 此题属于一次函数综合题,涉及的知识有:一次函数与坐标轴的交点,勾股定理,角平分线性质,以及等腰三角形的性质,利用了分类讨论的思想,熟练掌握定理及性质是解本题的关键.

 天天向上口算本系列答案
天天向上口算本系列答案| A. | 2,1,3 | B. | 2,1,-3 | C. | 2,-1,3 | D. | 2,-1,-3 |
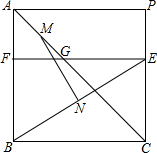 如图,四边形ABCD是边长为8的正方形,点E是CD上的一个动点,EF∥BC分别交AC,AB于点G,F,M,N分别是AG,BE的中点.
如图,四边形ABCD是边长为8的正方形,点E是CD上的一个动点,EF∥BC分别交AC,AB于点G,F,M,N分别是AG,BE的中点.