题目内容
6．求下列各式中x的值（1）（x+1）2-3=0；
（2）3x3+4=-20．
分析 根据立方根和立方根的性质即可求出x的值．
解答 解：（1）（x+1）2-3=0，
∴x+1=±$\sqrt{3}$，
解得：x1=-1+$\sqrt{3}$，x2=-1-$\sqrt{3}$；
（2）3x3+4=-20，
∴3x3=-24，
∴x3=-8，
解得：x=-2．
点评 本题考查立方根与平方根的性质，要注意一个正数的平方根由两个且互为相反数，任何一个数的立方根只有一个．
练习册系列答案
相关题目
3．下列运算中正确的是（ ）
| A． | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B． | 2$\sqrt{3}$+3$\sqrt{3}$=6$\sqrt{3}$ | C． | $\sqrt{6}$$÷\sqrt{2}$=$\sqrt{3}$ | D． | （$\sqrt{2}$+1）（$\sqrt{2}$-1）=3 |
1．下列方程的变形中，正确的是（ ）
| A． | 若y-4=8，则y=8-4 | |
| B． | 若2（2x-3）=2，则4x-6=2 | |
| C． | 若-$\frac{1}{2}$x=4，则x=-2 | |
| D． | 若 $\frac{1}{3}$-$\frac{t-1}{2}$=1，则去分母得2-3（t-1）=1 |
如图，在△ABC中，DE是AC的垂直平分线，AE=5cm，△ABC的周长为26cm，则△ABD的周长为16 cm．
18．
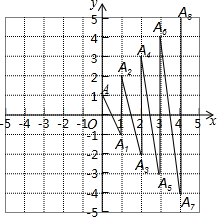如图在平面直角坐标系上有一点A（0，1），点A第一次跳动至点A1（1，-1），第二次由点 A1跳到点A2（1，2），第三次由点A2跳到A3（2，-2）…由此规律跳动下去，第80次跳到点A80的坐标是（ ）
如图在平面直角坐标系上有一点A（0，1），点A第一次跳动至点A1（1，-1），第二次由点 A1跳到点A2（1，2），第三次由点A2跳到A3（2，-2）…由此规律跳动下去，第80次跳到点A80的坐标是（ ）| A． | （40，40） | B． | （41，40） | C． | （40，41） | D． | （41，41） |
在△ABC中，AB=8，BC=10，AC=6，动点P从点C出发，沿着CB运动，速度为每秒2个单位，到达点B时运动停止，设运动时间为t秒，请解答下列问题：
16．下列运算中，正确的是（ ）
| A． | （x2）3=x5 | B． | x2+x3=x5 | C． | （x-y）2（y-x）3=（x-y）5 | D． | x2•x3=x5 |