题目内容
18.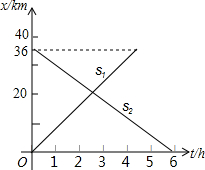 如图,甲、乙两人分别从A、B两地同时出发,相向而行.他们各自离A地的路程s1(km)、s2(km)与出发后的时间t(h)之间的函数关系如图7所示,结合图象回答下列问题:
如图,甲、乙两人分别从A、B两地同时出发,相向而行.他们各自离A地的路程s1(km)、s2(km)与出发后的时间t(h)之间的函数关系如图7所示,结合图象回答下列问题:(1)A、B两地的路程是36km,甲、乙行驶全程所用的时间分别为4.5h和6h;
(2)求甲、乙两人离A地的路程s1(km)、s2(km)与行驶时间t(h)之间的函数关系式;
(3)求图象交点的坐标,并解释交点的横坐标和纵坐标所表示的实际意义.
(4)求两直线与横轴围成的面积.
分析 (1)根据图象给出的数据可直接得出A、B两地的路程是36km,甲、乙行驶全程所用的时间分别为4.5h和6h;
(2)根据速度=$\frac{路程}{时间}$,先分别求出甲和乙的速度,再根据路程=速度×时间即可得出路程与行驶时间之间的函数关系式;
(3)根据两直线相交得出s1=s2,求出t的值,从而得出s=$\frac{144}{7}$m,即可得出交点坐标,并得出交点的横坐标和纵坐标所表示的实际意义;
(4)根据三角的面积公式代值计算即可.
解答 解:(1)从图象可知:A、B两地的路程是36km,甲、乙行驶全程所用的时间分别为4.5h和6h;
故答案为:36,4,6;
(2)由图知道:甲的速度是V甲=$\frac{S}{t}$=$\frac{36}{4.5}$=8km/h,乙的速度是V乙=$\frac{S}{t}$=$\frac{36}{6}$=6km/h,
则s1=8t;s2=36-6t;
(3)∵两直线相交,就是s1=s2,即8t=36-6t,
∴t=$\frac{18}{7}$h,
∴s=$\frac{144}{7}$m,
∴交点坐标为($\frac{18}{7}$,$\frac{144}{7}$),
∴横坐标表示在出发了$\frac{18}{7}$h这么长时间,纵坐标表示在离A地$\frac{144}{7}$m这么远的地方两人相遇;
(4)根据题意得:两直线与横轴围成的面积是:$\frac{1}{2}$×6×$\frac{144}{7}$=$\frac{432}{7}$(m2).
点评 此题考查了一次函数的综合,用到的知识点是速度=$\frac{路程}{时间}$,三角形的面积公式,关键是根据函数的图象,得出相关的数据.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
8.”造林见林,见林见效”这是退耕还林、造林的基本要求,更是农民的朴实愿望,四川省林业厅副厅长包建华说,退耕还林直补给退耕农户带来实惠,累计兑现政策性补助资金331.92亿元,户均5500元.将331.92亿用科学记数法表示为( )
| A. | 3.3192×108 | B. | 3.3192×109 | C. | 3.3192×1010 | D. | 3.3192×1011 |
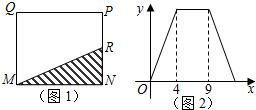 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.在这个变化过程中,变量x表示点R运动的路程,变量y表示△MNR的面积,图2表示变量y随x的变化情况,则当y=9时,点R所在的边是:PN边或QM边.
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.在这个变化过程中,变量x表示点R运动的路程,变量y表示△MNR的面积,图2表示变量y随x的变化情况,则当y=9时,点R所在的边是:PN边或QM边. 如图,某涵洞的截面是抛物线的一部分,现水面宽AB=1.6m,涵洞顶点O到水面的距离为2.4m,求涵洞所在抛物线的解析式.
如图,某涵洞的截面是抛物线的一部分,现水面宽AB=1.6m,涵洞顶点O到水面的距离为2.4m,求涵洞所在抛物线的解析式.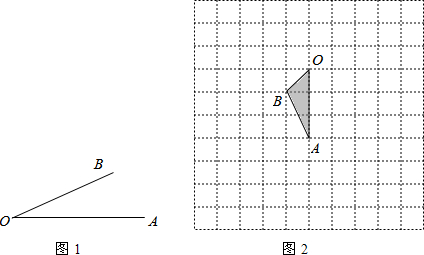
 如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )
如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点B′处,则BE的长为( )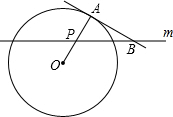 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线m,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
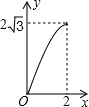
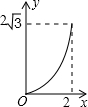
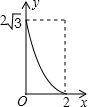
如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线m,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )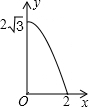
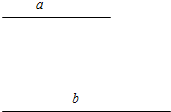 画图:已知线段a、b.
画图:已知线段a、b.