题目内容
 (1)如图,已知∠B+∠D=∠BED,求证:AB∥CD,
(1)如图,已知∠B+∠D=∠BED,求证:AB∥CD,证明:画∠BEF=∠B,∴AB∥EF
又∵∠B+∠D=∠BED=∠BEF+∠DEF
∴∠DEF=∠D,∴EF∥CD
∴AB∥CD.
(2)如图,已知∠B=25°,∠BCD=45°,∠CDE=30°,∠E=10°
仿(1)的证法:求证:AB∥EF.
考点:平行线的判定
专题:证明题
分析:作CM∥AB,作DN∥EF,先求出∠2=∠3,证出CM∥DN,即可证出AB∥EF.
解答:证明:(2)作CM∥AB,作DN∥EF,如图2所示:
 则∠1=∠B=25°,∠4=∠E=10°,
则∠1=∠B=25°,∠4=∠E=10°,
∵∠BCD=45°,∠CDE=30°,
∴∠2=∠BCD-∠1=20°,∠3=∠CDE-∠4=20°,
∴∠2=∠3,
∴CM∥DN,
又∵CM∥AB,DN∥EF,
∴AB∥EF.
 则∠1=∠B=25°,∠4=∠E=10°,
则∠1=∠B=25°,∠4=∠E=10°,∵∠BCD=45°,∠CDE=30°,
∴∠2=∠BCD-∠1=20°,∠3=∠CDE-∠4=20°,
∴∠2=∠3,
∴CM∥DN,
又∵CM∥AB,DN∥EF,
∴AB∥EF.
点评:本题考查了平行线的性质与判定的综合运用;通过作辅助线得出内错角相等是解决问题的关键;注意性质与判定的区别.

练习册系列答案
相关题目
如果两个相似三角形的面积比是1:4,那么它们的周长比是( )
A、1:
| ||
B、
| ||
| C、1:2 | ||
| D、1:4 |
函数表达式y=
中的自变量x取值范围是( )
| 1 | ||
|
| A、x≥2 | B、x≤2 |
| C、x>2 | D、x<2 |
 如图是一个多边形,求∠A1+∠A2+∠A3+…+∠A23+∠A24的度数.
如图是一个多边形,求∠A1+∠A2+∠A3+…+∠A23+∠A24的度数. 如图,△ABC中,AD是∠BAC的平分线,AD的垂直平分线AD交于点E,交BC的延长线于点F.试说明:△ABF∽△CAF.
如图,△ABC中,AD是∠BAC的平分线,AD的垂直平分线AD交于点E,交BC的延长线于点F.试说明:△ABF∽△CAF. 如图,已知A(-4,0.5),B(-1,2)是一次函数y=ax+b与反比例函数
如图,已知A(-4,0.5),B(-1,2)是一次函数y=ax+b与反比例函数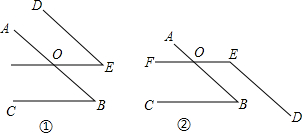
 如图,小明在河岸的A处观察对岸C处的一棵树,视线与河岸30°角;同时,小亮在距小明100米的河岸B观察对岸D处的一棵树,视线与河岸成75°角.已知河宽90米,且两岸平行,求河对岸C、D两棵树的距离.(参考数据:
如图,小明在河岸的A处观察对岸C处的一棵树,视线与河岸30°角;同时,小亮在距小明100米的河岸B观察对岸D处的一棵树,视线与河岸成75°角.已知河宽90米,且两岸平行,求河对岸C、D两棵树的距离.(参考数据: 已知:如图△ABC中,BD和CE是三角形的高,M为BC的中点,P为DE的中点.求证:PM⊥DE.
已知:如图△ABC中,BD和CE是三角形的高,M为BC的中点,P为DE的中点.求证:PM⊥DE.